The pseudopotential theory began as an extension of the OPW method. It is based on an ansatz which separates the total wave function into an oscillatory part and a smooth part, the so called pseudo wave function. The strong true potential of the ions is replaced by a weaker potential valid for the valence electrons.
Philips and Kleinman (1959) showed that one can construct a smooth valence function ![]() that is orthogonal to the core states
that is orthogonal to the core states ![]() , by using the following construction:
, by using the following construction:
| (219) |
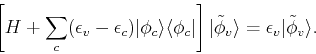 |
(220) |
| (221) |
| (222) |
To simplify the problem even further, model pseudopotentials are used in place of the actual pseudopotential, for instace:
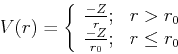 |
(223) |
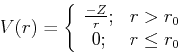 |
(224) |
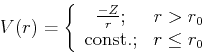 |
(225) |
The solution of the problem is very simple. All these pseudopotentials have to be Fourier transformed to obtain the coefficients ![]() , which are replaced in the OPW Schrödinger equation, which is in turn solved numerically.
, which are replaced in the OPW Schrödinger equation, which is in turn solved numerically.