 |
(226) |
As we have seen beofre, we can write the pseudopotential as a Fourier series:
 |
(226) |
In crystal structures that consist of more than one atom per unit cell, we need to introduce a structure factor ![]() , defined as
, defined as
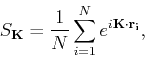 |
(227) |
| (228) |
In crystals with a diamond structure there are two atoms at the positions ![]() and
and ![]() in the primitive unit cell. By taking the midpoint between the two atoms in the unit cell as origin, the positions of the atoms are given by
in the primitive unit cell. By taking the midpoint between the two atoms in the unit cell as origin, the positions of the atoms are given by
![]() and
and
![]() . Thus, the structure factor is given by
. Thus, the structure factor is given by
| (229) |
In unstrained diamond structures the reciprocal lattice vectors in order of increasing magnitude are (in units of
![]() ):
):
| (230) | |||
| (231) | |||
| (232) | |||
| (233) | |||
| (234) |
Form factors with reciprocal lattice vectors larger than
![]() are neglected, since typically
are neglected, since typically
![]() decreases as
decreases as ![]() for large
for large ![]() . Assuming that the atomic pseudopotentials are spherically symmetric
. Assuming that the atomic pseudopotentials are spherically symmetric
![]() , the form factors only depend on the absolute value of the reciprocal lattice vector. The form factor belonging to
, the form factors only depend on the absolute value of the reciprocal lattice vector. The form factor belonging to ![]() shifts the entire energy scale by a constant value, and can therefore be set to zero. The form factors belonging to the reciprocal lattice vectors
shifts the entire energy scale by a constant value, and can therefore be set to zero. The form factors belonging to the reciprocal lattice vectors ![]() have an absolute value of
have an absolute value of
![]() and are conventionally labeled
and are conventionally labeled ![]() . Since the structure factor of the reciprocal lattice vectors
. Since the structure factor of the reciprocal lattice vectors ![]() with magnitude
with magnitude
![]() vanishes,
vanishes,
| (235) |
In Table 5.4.2 the parameters employed in the empirical pseudopotential calculations are listed. They consist of three local form factors
![]() .
.