Matrix elements

The basis is orthonormal. This implies that:

$$S_{{\bf K},{\bf K}'}^{\bf k} = \delta_{{\bf K},{\bf K}'}$$ (212)

$$T_{{\bf K},{\bf K}'}^{\bf k} = -\frac{\hbar^2}{2m}\langle \phi_{\bf K}^{\bf k}\vert\nabla^2\vert... ...k} \rangle = \frac{\hbar^2}{2m} \vert{\bf k+K}\vert^2 \delta_{{\bf K},{\bf K}'}$$ (213)

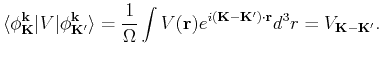$$V_{{\bf K},{\bf K}'}^{\bf k} = \langle \phi_{\bf K}^{\bf k}\vert V\vert\phi_{\bf K'}^{\bf k} \ra... ...ac{1}{\Omega}\int V({\bf r})e^{i{\bf (K-K')}\cdot {\bf r}} d^3r = V_{\bf K-K'}.$$ (214)

Hence, we obtain the following expression for the Schrödinger equation:

$$\sum_{\bf K'} \left(\frac{\hbar^2}{2m} \vert{\bf k+K}\vert^2... ...ght) C_{\bf k}({\bf K'}) = \epsilon_{\bf k} C_{\bf k}({\bf K})$$ (215)

A realistic calculation should include a large number of terms in the series, but usually it is necessary to impose a cutoff energy:

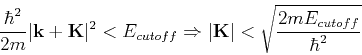$$\frac{\hbar^2}{2m}\vert{\bf k+K}\vert^2 < E_{cutoff} \Rightarrow \vert{\bf K}\vert < \sqrt{\frac{2mE_{cutoff}}{\hbar^2}}$$ (216)