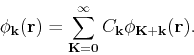Next: Matrix elements
Up: Methods for band-structure calculations
Previous: Limitations of the tight-binding
From Bloch's theorem we know that
 |
(205) |
where the function 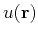 is a periodic function with the periodicity of the lattice.
This means that we can always expand it in a Fourier series as
is a periodic function with the periodicity of the lattice.
This means that we can always expand it in a Fourier series as
 |
(206) |
where 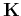 is a vector of the recirpocal lattice.
is a vector of the recirpocal lattice.
Let us define the PW basis as
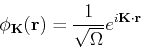 |
(207) |
We can see that this is an orthonormal basis
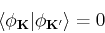 |
(208) |
We can now write the wave function  in this basis as:
in this basis as:
 |
(209) |
We can redefine the basis by including the phase in the exponential
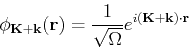 |
(210) |
to obtain
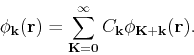 |
(211) |
Subsections



Next: Matrix elements
Up: Methods for band-structure calculations
Previous: Limitations of the tight-binding
Adrian E. Feiguin
2009-11-04

![]() in this basis as:
in this basis as: