Introduction

We are interested in calculating the ground state energy of a generic Hamiltonian for a system of many electons interacting with an external potential $V_{ext}({\bf r})$. We assume this external potential depends only on the coordinates ${\bf r}$, and it is generaly given by the interaction with the nuclei, as we have seen in previous sections. Therefore the Hamiltonian reads: For a many-body system, the Hamiltonian is given by

$$H = \sum_i \left[\frac{1}{2}\nabla_i^2+V_{ext}({\bf r}_i)\right] + \sum_{i,j>i} \frac{1}{\vert{\bf r} - {\bf r}_j\vert}$$ (118)

$$= T+V_{ext}+V_{e-e},$$ (119)

where we have also included the electron-electron interactions. $V_{ext}$ is an external potential, which, in systems of interest to us, is the Coulomb attraction by the nuclei.

The kinetic energy and the external potential are one-particle terms, while the electron-electron term is a two-body interaction. We can rewrite the energy as

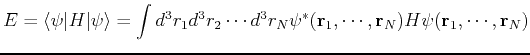$$E = \langle \psi \vert H\vert \psi \rangle = \int d^3r_1d^3r_2 \cdots d^3r_N \psi^*({\bf r}_1,\cdots,{\bf r}_N) H \psi({\bf r}_1,\cdots,{\bf r}_N)$$ (120)

$$= N\int d^3r_1d^3r_2 \cdots d^3r_N \psi^*({\bf r}_1,\cdots,{\bf r}_N)\left[T({\bf r}_1)+V_{ext}({\bf r}_1)\right]\psi({\bf r}_1,\cdots,{\bf r}_N) +$$ (121)

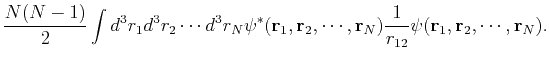$$\frac{N(N-1)}{2}\int d^3r_1d^3r_2\cdots d^3r_N \psi^*({\bf r}_1,{... ...,\cdots,{\bf r}_N) \frac{1}{r_{12}} \psi({\bf r}_1,{\bf r}_2,\cdots,{\bf r}_N).$$ (122)

Let us define the density matrix as

$$g({\bf r}_1,{\bf r}_2,{\bf r}_1',{\bf r}_2') = \int d^3r_3d^... ...\cdots,{\bf r}_N) \psi({\bf r}_1',{\bf r}_2',\cdots,{\bf r}_N)$$ (123)

and the pair-correlation as

$$g({\bf r}_1,{\bf r}_1') = \int d^3r_2d^3r_3\cdots d^3r_N \ps... ... r}_2,\cdots,r_N) \psi({\bf r}_1',{\bf r}_2,\cdots,{\bf r}_N).$$ (124)

and the density as:

$$n(r) = \int d^3r_2d^3r_3\cdots d^3r_N \psi^*({\bf r},{\bf r}_2,\cdots,{\bf r}_N) \psi({\bf r},{\bf r}_2,\cdots,{\bf r}_N).$$ (125)

We can now write the interaction part of the enrgy as:

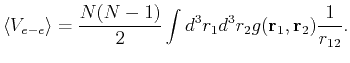$$\langle V_{e-e} \rangle = \frac{N(N-1)}{2}\int d^3r_1d^3r_2 g({\bf r}_1,{\bf r}_2) \frac{1}{r_{12}}.$$ (126)

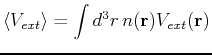$$\langle V_{ext} \rangle = \int d^3r n({\bf r}) V_{ext}({\bf r})$$ (127)

What's noteworthy about these expression is that we do not need the wave-function to calculate this quantity, we only need the density and the pair-correlation function, which is complicated, or even impossible to evaluate.

Density Functional Theory goes a step further, and it states that we can evaluate the energy if we just know the density.

Thsi is a remarkable result, and the implications are very powerful: we know that wafe-functions are very complicated objects compared to the density. Working with the density simplifies the problem enormously. However, we notice right away that we have avoided writing the kinetic energy and the interaction energies as fcuntiosn of the density. This is because we simply do not know how to do it! Density functional theory hints at a method to get good guesses by using the so-called Kohn-Sham equations, and the local density approximation, and this is what we are going to leanr in the course of this section.