| (128) |
The pair correlation function satisfies a very important sum-rule:
| (128) |
The effect of the pair correlation is to keep the particles appart by virtue of the interaction and Pauli's exclusion principle. Of these, we expect the interaction to give the larger contribution. In fact, setting ![]() amounts to the Hartree potential, whcih neglects all effects of exchange and correlation, but still takes Coulomb repulsion into account. Furthermore, we expect that at large distances the particles interact very weakly, thus
amounts to the Hartree potential, whcih neglects all effects of exchange and correlation, but still takes Coulomb repulsion into account. Furthermore, we expect that at large distances the particles interact very weakly, thus
![]() as
as
![]() . These observations lead us to separating
. These observations lead us to separating ![]() into two contrubutions by rewriting
into two contrubutions by rewriting ![]() , whcih will give us one pure interaction term -or Hartree term -- from the first
, whcih will give us one pure interaction term -or Hartree term -- from the first ![]() and one, hopefully small exchange correlation term from the
and one, hopefully small exchange correlation term from the ![]() :
:
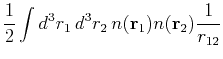 |
(129) | ||
 |
(130) |
At this point it is appropriate to say a few words about the Hartree-Fock approximation, in which exchange is taken into account by requiring all wavefunctions to be Slater determinants. It still ignores the correlation energy, whcih can be defined as exactly that: everything that is ignored in Hartree-Fock.