|
Abstract: The purpose of this talk is to describe the class of functions 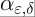 mentioned in the title. These functions satisfy certain integral inequalities and play an important role in the solution of the quantitative Oppenheim conjecture (counting integer solutions of quadratic inequalities), in the study of recurrence properties of random walks on homogeneous spaces, and in an alternate approach to the proof of the theorem of Borel and Harish-Chandra on the finiteness of covolumes of arithmetic subgroups. mentioned in the title. These functions satisfy certain integral inequalities and play an important role in the solution of the quantitative Oppenheim conjecture (counting integer solutions of quadratic inequalities), in the study of recurrence properties of random walks on homogeneous spaces, and in an alternate approach to the proof of the theorem of Borel and Harish-Chandra on the finiteness of covolumes of arithmetic subgroups.
|