Brandeis-Harvard-MIT-Northeastern
JOINT MATHEMATICS COLLOQUIUM
| Holomorphic flexibility of complex manifolds |
Dror Bar-Nathan
University of Toronto
Harvard University
Thursday, October 28, 2004
Talk at 4:30 p.m. in Science Center D
Tea at 4:00 p.m. in the Math Lounge
|
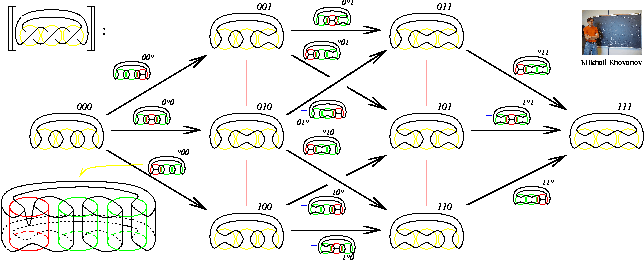
Abstract: In my talk I will display one complicated picture and discuss it at length, finding that it's actually quite simple. Applying a certain 2D TQFT, we will get a homology theory whose Euler characteristic is the Jones polynomial. Not applying it, very cheaply we will get an invariant of tangles which is functorial under cobordisms and an invariant of 2-knots. Why is it interesting?
The picture:
|
|
|
Web page: Alexandru I. Suciu |
Comments to: alexsuciu@neu.edu |
| Posted: March 10, 2004 | URL: http://www.math.neu.edu/bhmn/forstneric04.html |