The current organizer of the seminar is Maxim Braverman.

• April 7,  2023
  Speaker:  Ian Montague (Brandeis )
  Title: TBA
  Abstract: TBA

• March 31,  2023
  Speaker:  Ali Maalaoui (Clark)
  Title: Q'-curvature and Spectra on Pseudo-Einstein 3-manifolds
  Abstract: In this talk I will present a link between the CR Beckner-Onofri type inequality proved by Branson-Fontana-Morpurgo and the spectral invariants of the P'-operator related to prescribing the Q'-curvature. This link can be tracked on one hand through the computation of the functional determinant of P', namely ζ'_P' (0) and on the other hand through the logarithmic Hardy-Littlewood-Sobolev inequality, namely the regularized zeta function at 1

• February 10,  2023
  Speaker:  Xuwen Zhu (Northeastern)
  Title: Spectral gaps for large genus hyperbolic surfaces
  Abstract: The study of "small" eigenvalues of the Laplacian on hyperbolic surfaces has a long history and has recently seen many developments. In this talk I will focus on the recent work (joint with Yunhui Wu and Haohao Zhang) on the higher spectral gaps, where we study the differences of consecutive eigenvalues up to   for genus g hyperbolic surfaces. We show that the supremum of such spectral gaps over the moduli space has infimum limit at least 1/4 as genus goes to infinity. The analysis relies on previous joint works with Richard Melrose on degenerating hyperbolic surfaces.
  
  

• January 27,  2023
  Speaker:  Ahmad Reza Haj Saeedi Sadegh (Northeastern)
  Title: Rescaling method and a fixed-point formula for Dirac operators on groupoids
  Abstract: Inspired by Pflaum-Posthuma-Tang, Heitsch-Lazarov, and Connes-Skandalis, we give a fixed-point formula for the equivariant index of source-wise Dirac operators on Lie Groupoids. For the proof, we use Getzler's rescaling argument with a deformation space technique, as in Higson-Yi and the joint work with Braverman.

• December 2,  2022
  Speaker:       Tina Torkaman (Harvard)
  Title:  Intersection number and intersection points of closed geodesics on hyperbolic surfaces
  Abstract: In this talk, I will talk about the (geometric) intersection number between closed geodesics on finite volume hyperbolic surfaces. Specifically, I will discuss the optimum upper bound on the intersection number in terms of the product of hyperbolic lengths. I also talk about the equidistribution of the intersection points between closed geodesics.

• November 18,  2022
  Speaker:       Robert Ream (Clark University)
  Title: Almost Kahler Manifolds dual to PP-wave Spacetimes
  Abstract: We will give a brief description of PP-waves, and show how they can be deformed by their propagation wave vector to give an almost-Kahler Riemannian metric. These almost-Kahler metrics exist in all dimensions 2n≥ 4​​, and are defined on both ℝ^2n​​ and 𝕊¹x𝕊¹ x M​​, where M is any closed almost-Kahler manifold.  We will then discuss Lejmi and Shen's use of this construction to produce extremal-almost Kahler metrics and second-Chern-Einstein almost Kahler metrics.

• November 4,  2022
  Speaker:   Giada Franz (MIT)
  Title: On the stability of minimal submanifolds in conformal spheres
  Abstract: A minimal submanifold of a compact Riemannian manifold is defined as a critical point of the volume functional. We say that such a submanifold is stable if the second derivative of the volume is nonnegative.
  In 1968, Simons proved that there are no stable minimal submanifolds in the round sphere of any dimension. A few years later, Lawson and Simons conjectured that the same holds in every compact Riemannian manifold that is 1/4-pinched.
  In this talk, we will give an overview on this problem, which is still open in its full generality, and we will present a partial result, which is joint work with Federico Trinca, in the case when the ambient manifold is conformal to the round sphere.​
  

• October 14,  2022
  Speaker:  Robert McOwen (Northeastern)
  Title: The Fundamental Solution of an Elliptic Equation with Singular Drift
  Abstract: For n≥3, we study the existence and asymptotic properties of the fundamental solution for elliptic operators in nondivergence form, L(x,∂x)=a_ij(x)∂_i∂_j+b_k(x)∂^k, where the a_ijhave modulus of continuity ω(r) satisfying the square-Dini condition and the bk are allowed mild singularities of order r⁻¹ω(r). A singular integral is introduced that controls the existence of the fundamental solution. We give examples that show the singular drift b_k∂^k may act as a perturbation that does not dramatically change the fundamental solution of L^o=a_ij∂_i∂_j, or it could change an operator L^o that does not have a fundamental solution to one that does.

• November 12,   2021
  Speaker:  Jie (Frank) Xu (Boston University)
  Title: Yamabe Problem on Various Domains
  Abstract:

                                

• October 8,  2021
  Speaker:  Ahmad Reza Haj Saeedi Sadegh (Northeastern)
  Title: Deformation to the Normal Cone and its Applications
  Abstract: We will import the notion of deformation to the normal cone from algebraic geometry to differential geometry. This notion has direct and indirect applications in symplectic geometry, Morse theory and Getzler's calculus in index theory.

• October 1,  2021
  Speaker:  Teng Fei (Rutgers)
  Title: The Type IIA flow and its applications in symplectic geometry
  Abstract: The equations of flux compactifications of Type IIA superstrings were written down by Tomasiello and Tseng-Yau. To study these equations, we introduce a natural geometric flow on symplectic Calabi-Yau 6-manifolds. We prove
  the well-posedness of this flow and establish the basic estimates. We show that the Type IIA flow can be applied to find optimal almost complex structures on certain symplectic manifolds. This is based on joint work with Phong, Picard and Zhang.
  

• April 23,  2021
  Speaker:  Lorenzo Brandolese (Institut Camille Jordan)
  Title: Geometric structures of 2D Navier-Stokes flows
  Abstract: Geometric structures naturally appear in fluid motions. One of the best known examples is Saturn’s Hexagon <https://fr.wikipedia.org/wiki/Hexagone_de_Saturne#/media/Fichier:PIA20513_-_Basking_in_Light.jpg>, the huge cloud pattern at the level of Saturn’s north pole, remarkable both for the regularity of its shape and its stability during the past decades. In this paper we will address the spontaneous formation of hexagonal structures in planar viscous flows, in the classical setting of Leray’s solutions of the Navier–Stokes equations. Our analysis also makes evidence of the isotropic character of the energy density of the fluid for sufficiently localized 2D flows in the far field: it implies, in particular, that fluid particles of such flows are nowhere at rest at large distances.

• December 4,  2020
  Speaker:  Charles Ouyang (U. Mass Amherst)
  Title: Length spectrum compactification of the SL(3,R)-Hitchin component
  Abstract: Hitchin components are natural generalizations of the classical Teichmüller space. In the setting of SL(3,R), the Hitchin component parameterizes the holonomies of convex real projective structures. By
  studying Blaschke metrics, which are Riemannian metrics associated to such structures, along with their limits, we obtain a compactification of the SL(3,R) Hitchin component. We show the boundary objects are hybrid
  structures, which are in part flat metric and in part laminar. These hybrid objects are natural generalizations of measured laminations, which are the boundary objects in Thurston's compactification of Teichmüller space. (joint work with Andrea Tamburelli)

• November 20,  2020
  Speaker:  Laura Fredrickson (U. of Oregon) video of the talk
  Title: The asymptotic geometry of the Hitchin moduli space
  Abstract: Hitchin's equations are a system of gauge theoretic equations on a Riemann surface that are of interest in many areas including representation theory, Teichm\"uller theory, and the geometric Langlands correspondence. The Hitchin moduli space carries a natural hyperk\"ahler metric.  An intricate conjectural description of its asymptotic structure appears in the work of Gaiotto-Moore-Neitzke and there has been a lot of progress on this recently.  I will discuss some recent results using tools coming out of geometric analysis which are well-suited for verifying these extremely delicate conjectures. This strategy often stretches the limits of what can currently be done via geometric analysis, and simultaneously leads to new insights into these conjectures.

• November 13,  2020
  Speaker:  Hadrian Quan (Urbana-Champaign) video of the talk
  Title: Sub-Riemannian Limit of the differential form heat kernels of contact manifolds
  Abstract: We present work investigating the behavior of the heat kernel of the Hodge Laplacian on a contact manifold endowed with a family of Riemannian metrics that blow-up the directions transverse to the contact distribution. We apply this to analyze the behavior of global spectral invariants such as the η-invariant and the determinant of the Laplacian. In particular we prove that contact versions of the relative η-invariant and the relative analytic torsion are equal to their Riemannian analogues and hence topological. (Joint work with Pierre Albin)
  

• November 6,  2020
  Speaker:   Misha Karpukhin (Irvine)       video of the talk
  Title: Eigenvalues of the Laplacian and min-max for the energy functional
  Abstract: The Laplacian is a canonical second order elliptic operator defined on any Riemannian manifold. The study of optimal upper bounds for its eigenvalues is a classical problem of spectral geometry going back to J. Hersch, P. Li and S.-T. Yau. It turns out that the optimal isoperimetric inequalities for Laplacian eigenvalues are closely related to minimal surfaces and harmonic maps. In the present talk we survey recent developments in the field. In particular, we will discuss a min-max construction for the energy functional and its applications to eigenvalue inequalities, including the regularity theorem for optimal metrics. The talk is based on the joint work with D. Stern.

• October 30,  2020
  Speaker:    Simone Cecchini  (University of  Goettingen)    video of the talk
  Title: A long neck principle for Riemannian spin manifolds with positive scalar curvature
  Abstract: We present results in index theory on compact Riemannian spin manifolds with boundary in the case when the topological information is encoded by bundles which are supported away from the boundary.
  As a first application, we establish a ``long neck principle'' for a compact Riemannian spin n-manifold with boundary X, stating that if scal(X) ≥ n(n-1) and there is a nonzero degree map f into the n-sphere which is area decreasing, then the distance between the support of the differential of f and the boundary of X is at most π/n. This answers, in the spin setting, a question recently asked by Gromov.
  As a second application, we consider a Riemannian manifold X obtained by removing a small n-ball from a closed spin n-manifold Y. We show that if scal(X) ≥ σ >0 and Y satisfies a certain condition expressed in terms of higher index theory, then the width of a geodesic collar neighborhood Is bounded from above from a constant depending on σ and n.
  Finally, we consider the case of a Riemannian n-manifold V diffeomorphic to Nx [-1,1], with N a closed spin manifold with nonvanishing Rosenebrg index.
  In this case, we show that if scal(V) ≥ n(n-1), then the distance between the boundary components of V is at most 2π/n. This last constant is sharp by an argument due to Gromov.

• October 23,  2020
  Speaker:   Yiannis Loizides  (Cornell)  
  Title: Hamiltonian loop group spaces and a theorem of Teleman-Woodward video of the talk
  Abstract: Using algebro-geometric methods, Teleman and Woodward proved an interesting index formula (generalizing the Verlinde formula) for the moduli space of G-bundles on a closed Riemann surface. I will describe an approach to reformulating and generalizing their theorem to the smooth setting.

• October 16,  2020
  Speaker:   Vladimir E. Nazaikinskii (Ishlinsky Institute for Problems in Mechanics, Moscow)  
  Title: Partial spectral flow and the Aharonov-Bohm effect in graphene video of the talk
  Abstract: We study the Aharonov-Bohm effect in an open-ended tube made of a graphene sheet whose dimensions are much larger than the interatomic distance in graphene. An external magnetic field
  vanishes on and in the vicinity of the graphene sheet, and its flux through the tube is adiabatically switched on. It is shown that, in the process, the energy levels of the tight-binding Hamiltonian of π-electrons unavoidably cross the Fermi level, which results in the creation of electron-hole pairs. The number of pairs is proven to be equal to the number of magnetic flux quanta of the external field. The proof is based on the new notion of partial spectral flow, which generalizes the ordinary spectral flow already having well-known applications (such as the Kopnin forces in superconductors and superfluids) in condensed matter physics. (joint work with Mikhail I. Katsnelson)
  

• October 9,  2020
  Speaker:     Shu Shen ( Jussieu)  
  Title: Complex-valued analytic torsion and the dynamical zeta function video of the talk
  Abstract: The relation between the spectrum of the Laplacian and the closed geodesics on a closed Riemannian manifold is one of the central themes in differential geometry. Fried conjectured that the analytic torsion, which is an alternating product of regularized determinants of the Laplacians, equals the zero value of the dynamical zeta function.  In this talk, I will explain a recent work on a relation between the complex valued analytic torsion and the dynamical zeta function with arbitrary twist on locally symmetric space, which generalises the previous result of myself for unitary twists, and the results of Müller and Spilioti on hyperbolic manifolds.
  
  

• October 2,  2020
  Speaker:     Marina Prokhorova (Technion)  
  Title: Family index for self-adjoint elliptic operators on surfaces with boundary video of the talk
  Abstract: An index theory for elliptic operators on a closed manifold was developed by Atiyah and Singer. For a family of such operators parametrized by points of a compact space X, they computed the K⁰ (X)-valued analytical index in purely topological terms. An analog of this theory for self-adjoint elliptic operators on closed manifolds was developed by Atiyah, Patodi, and Singer; the analytical index of a family in this case takes values in the K¹ group of a base space.
     If a manifold has non-empty boundary, then boundary conditions come into play, and situation becomes much more complicated. The integer-valued index of a single boundary value problem was computed by Atiyah, Bott, and Boutet de Monvel. This result was recently generalized to K⁰ (X)-valued family index by Melo, Schrohe, and Schick. The self-adjoint case, however, remained open.
     In the talk I shall present a family index theorem for self-adjoint elliptic operators on a surface with boundary. I consider such operators with self-adjoint elliptic local boundary conditions.   Both operators and boundary conditions are parametrized by points of a compact space X. I compute the K¹ (X)-valued analytical index of such a family in terms of the topological data of the family over the boundary. A particular case of this result is the spectral flow formula for one-parameter families of boundary value problems.

• September 25,  2020
  Speaker:    Zhu, Xuwen  (Northeastern)  
  Title: Spectral properties of spherical conical metrics
  Abstract: This talk will focus on the recent works on the spectral properties of constant curvature metrics with conical singularities on surfaces. The motivation comes from earlier works joint with Rafe Mazzeo
  on the study of deformation of such spherical metrics with large cone angles, which suggests that there is a deep connection between the geometric properties of the moduli space and the analytical properties of the associated singular Laplace operator. In this talk I will talk about a joint work with Bin Xu on spectral characterization of the monodromy of such metrics, and work in progress with Mikhail Karpukhin on the relation of spectral properties with harmonic maps.
  

Fall 2019

• November 22,  2019 at 12:45 (Note unusual time)
  Speaker:    Simone Cecchini  (University of  Göttingen)  
  Title: Localized obstructions to metrics of positive scalar curvature
  Abstract: We define a new obstruction to the existence of metrics of positive scalar curvature on a compact spin manifold with boundary X. More precisely, we define a topological invariant contained in a set K that doesn’t intersect the boundary. We show, using index theory, that the non vanishing of this invariant dictates a balance between the lower bound of the scalar curvature of X and the distance between K and the boundary of X. As an application, we obtain, in the spin setting, a solution to the “long neck problem”, recently proposed by Gromov. This is joint work with Thomas Schick.

• November 15,  2019
  Speaker:    Zuoqin Wang  (University of Science and Technology of China)  
  Title: On the remainders in the two-term Weyl law of planar disks and annuli
  Abstract: Weyl laws relate the asymptotic behaviors of the eigenvalues of certain geometric operators with the geometric/analytic/dynamical properties of the underline space. In this talk I will briefly describe these connections, with an emphasis on the relation between the eigenvalue counting problem for special planar domains with integrable billiard flows and the classical lattice points counting problem. This talk is based on joint works with Jingwei Guo, Wolfgang Müller and Weiwei Wang.

• November 8,  2019
  Speaker:    Nikhil Savale  (University of Cologne)  
  Title: Bochner Laplacian and Bergman kernel expansion of semi-positive line bundles on a Riemann surface
  Abstract: We generalize the results of Montgomery for the Bochner Laplacian on high tensor powers of a line bundle. When specialized to Riemann surfaces, this leads to the Bergman kernel expansion and geometric quantization results for semi-positive line bundles whose curvature vanishes at finite order. The proof exploits the relation of the Bochner Laplacian on tensor powers with the sub-Riemannian (sR) Laplacian.

• October 25, 2019
  Speaker:    Michael Levitin  (University of Reading)  
  Title: Asymptotics of Steklov eigenvalues for curvilinear polygons
  Abstract: I will discuss sharp asymptotics of large Steklov eigenvalues for planar curvilinear polygons. The asymptotic expressions for eigenvalues are given in terms of roots of some trigonometric polynomials which depend explicitly on the side lengths and angles of the polygon.
     It turns out that both the eigenvalue asymptotics and the corresponding quasimodes  depend non-trivially on the arithmetic properties of the angles of the  polygon, and are also related to the eigenvalues of a particular quantum graph. The proofs involve some classical hydrodynamics results related to a sloping beach problem, and a sloshing problem. I’ll also state some open questions. The talk will be based on joint works with Leonid Parnovski, Iosif Polterovich, and David Sher, see arXiv:1908.06455 and arXiv:1709.01891.

• October 4, 2019
  Speaker:    Alexander Moll  (Northeastern)  
  Title:  Soliton Quantization and Random Partitions
  Abstract: In this talk we present exact Bohr-Sommerfeld quantization conditions for the multi-phase and multi-soliton solutions of the classical Benjamin-Ono equation.  As an application, we use the theory of coherent states to construct a distinguished regularization of the critical Benjamin-Ono Cauchy problem with random periodic initial data sampled from a log-correlated Gaussian field.  We find that the conserved quantities of the random multi-phase solutions in our regularization define Jack measures on partitions, a special case of Borodin-Corwin’s Macdonald measures.  As a consequence, we realize old and new asymptotic results for random partitions as semi-classical and small dispersion asymptotics of our regularization. Our results suggest that random matrix universality captures quantum corrections to the well-known edge and bulk universality for classical dispersive shock waves.

• September 27, 2019
  Speaker:    Rudy Rodsphon  (Northeastern)  
  Title:  A K(K)-theoretical perspective on localization principles
  Abstract: In the 80’s, Witten introduced a deformation of the de Rham operator by a Morse function, which localizes the de Rham complex near the critical points of the Morse function. This principle has been widely extended to other contexts, notably in analytic proofs of the quantization commutes with reduction problem, in which such perturbations are used to localize the equivariant index of a Dirac operator near the critical points of a certain vector field coming from the action a Lie group. This phenomenon has a quite simple functorial explanation in K(K)-theory, that we will try to provide in the talk. We will also try to make the talk reasonably accessible.

• September 13, 2019
  Speaker:     Robert Chang (Northeastern)  
  Title: Quantum Ergodicity of Spherical Harmonics
  Abstract: The quantum ergodicity (QE) theorem relates the asymptotic behavior of eigenstates of a quantum system to the dynamics of the underlying Hamiltonian system. In particular, if the geodesic flow is ergodic, then the Laplace eigenfunctions must become ``equidistributed in phase space.'' On a round sphere, where the geodesic flow is completely integrable, the standard Laplace eigenfunctions (i.e., the standard spherical harmonics) do not equidistribute. We discuss how, in spite of the deterministic eigenfunctions being highly concentrated, random eigenfunctions enjoy the phase-space-equidistribution property almost surely.

• April 12, 2019
  Speaker:    Daniel Ruberman  (Brandeis)  
  Title: Obstructions to cobordisms of positive scalar curvature metrics
  Abstract: A classic problem in differential geometry asks when a given smooth manifold admits a Riemannian metric of positive scalar curvature. Topological obstructions to the existence come from (at least) two sources: index theory of the Dirac operator, and the study of volume-minimizing hypersurfaces. One can further ask for classification results, up to isotopy or even cobordism of such metrics. In this talk I will explain some recent work showing how to combine the two classic techniques to show that the cobordism groups of positive scalar curvature metrics can be infinite in dimensions 4 and 6. The proof uses a construction of volume-minimizing hypersurfaces with boundary (Botvinnik-Kazaras) and the end-periodic index theory of Mrowka-Ruberman-Saveliev.

• April 5, 2019
  Speaker:    Yiannis Loizides  (Penn State University)  
  Title: Witten deformation for Hamiltonian loop group spaces
  Abstract:  I will describe an approach to the quantization problem for Hamiltonian loop group spaces, how to do `Witten deformation' in this context, and the relation with the quantization-commutes-with-reduction theorem.  This is joint work with Yanli Song and Eckhard Meinrenken.

• March 29, 2019
  Speaker:    John Toth  (McGill University)  
  Title: Pointwise bounds for joint eigenfunctions of quantum completely integrable (QCI) systems
  Abstract: I will discuss some recent results on improvements in supremum bounds for joint eigenfunctions of QCI systems together with sharp exponential decay estimates  away from the projections of invariant Lagrangian tori (ie. in the microlocally forbidden region).  This is joint work with Jeff Galkowski.
  

• March 22, 2019
  Speaker:    Gideon Maschler  (Clark University)  
  Title: Kahler geometry on some Lorentzian 4-manifolds
  Abstract: We describe a construction of Kahler metrics on regions of an oriented 4-manifold equipped with a semi-Riemannian metric and two vector fields satisfying certain properties. Various Lorentzian examples of this will be given, in most of which the domain of definition of such a Kahler metric  coincides with the entire manifold. If time permits, we will: give conditions guaranteeing such a Kahler metric has zero Ricci determinant or is Einstein, along with examples; and sketch how to study curvature-distinguished metrics  directly using similar methods.

• March 15, 2019
  Speaker:    Saif Sultan  (Northeastern)  
  Title: Spatial asymptotic expansion of Euler equation without log terms
  Abstract: We will discuss how Euler equation preserves certain function spaces that have asymptotic expansions. Such asymptotic function spaces are known to have asymptotic terms that include logarithms. In 2 dimensional fluid flow complex number structure can be used to find smaller function spaces without log terms. We will study Cauchy operator on these asymptotic spaces. Finally we will show how this can be generalized to 3 and higher dimensions.

• November 30, 2018
  Speaker:   Maxim Braverman  (Northeastern University)  
  Title: The spectral Flow of a family of Toeplitz operators
  Abstract: We show that the (graded) spectral flow of a family of Toeplitz operators on a complete Riemannian manifold is equal to the index of a certain Callias-type operator. When the dimension of the manifold is even this leads to a cohomological formula for the spectral flow. As an application, we compute the spectral flow of a family of Toeplitz operators on a strongly pseudoconvex domain in Cn. This result is similar to the Boutet de Monvel's computation of the index of a single Toeplitz operator on a strongly pseudoconvex domain. Finally, we show that the bulk-boundary correspondence in a tight-binding model of topological insulators is a special case of our result.
  

• October 19, 2018
  Speaker:    Peter Crooks  (Northeastern University)  
  Title: Hyperkähler slices and spherical geometry
  Abstract: Hyperkähler manifolds have come to be studied in a number of contexts, including algebraic geometry, geometric analysis, symplectic geometry, and theoretical physics. Examples are often produced via the hyperkähler quotient construction, an analogue of symplectic reduction for a hyperkähler manifold equipped with a tri-Hamiltonian group action and a hyperkähler moment map. However, it is sometimes difficult to describe the hyperkähler moment map for purposes of deducing elementary facts about the quotient. One instance is the problem of deciding whether a given hyperkähler quotient is non-empty.
     I will discuss ongoing joint results with Maarten van Pruijssen concerning the emptiness / non-emptiness issue for a special class of hyperkähler quotients, called hyperkähler slices. Time-permitting, I will explain the manifestation of spherical geometry in our work. All relevant terms will be defined along the way.

• September 28, 2018
  Speaker:    Dmitry Jakobson  (McGill University)  
  Title: Large covers and sharp resonances of hyperbolic surfaces
  Abstract: First, we give a survey of results about distribution of resonances for hyperbolic surfaces. Then, I will discuss recent joint work with Frederic Naud and Louis Soares, where we study behaviour of resonances for large degree covers. Using techniques of thermodynamic formalism and representation theory, we prove new existence results of "sharp non-trivial resonances" in the large degree limit, for abelian covers and infinite index congruence subgroups.
  
  

• September 21, 2018
  Speaker:    Jeffrey Galkowski  (Northeastern) 
  Title: A novel approach to quantitative improvements for eigenfunction averages
  Abstract: In this talk we relate concentration of Laplace eigenfunctions in position and momentum to sup-norms and submanifold averages. In particular, we present a unified picture for sup-norms and submanifold averages which characterizes the concentration of those eigenfunctions with maximal growth. We then exploit this characterization to derive geometric conditions under which maximal growth cannot occur. Moreover, we obtain quantitative gains in a variety of geometric settings.

• September 14, 2018
  Speaker:    Rudy Rodsphon (Northeastern) 
  Title: On a conjecture of Connes and Moscovici
  Abstract: In the early eighties, Connes developed his Noncommutative Geometry program, mostly to extend index theory to situations where usual tools of differential topology are not applicable. A typical situation is foliations whose holonomy does not necessarily preserve any transverse measure, or equivalently the orbit space of the action of the full group of diffeomorphisms of a manifold. In the end of the nineties, Connes and Moscovici worked out an equivariant index problem in these contexts, and left a conjecture about the calculation of this index in terms of characteristic classes. The aim of this talk will be to survey the history of this problem, and time permitting, explain our recent solution to this conjecture. No prior knowledge of the subject will be assumed. This is a joint work with Denis Perrot

• March 30, 2018
  Speaker:    Simone Cecchini  (Universität Göttingen)
  Title: Enlargeability and positive scalar curvature on non-spin manifolds  
  Abstract: It is a classical result of Gromov and Lawson that enlargeable spin manifolds cannot carry metrics of positive scalar curvature. I will discuss how to extend this result to the case of non-spin manifolds. We make use of techniques on minimal hypersurfaces with singularities recently developed by Schoen and Yau. This is a joint work with Thomas Schick.

• February 16, 2018
  Speaker:    Amir Aazami (Clark University)
  Title:    Kähler metrics via Lorentzian geometry in dimension four
  Abstract: Given a semi-Riemannian 4-manifold (M,g) with two distinguished vector fields satisfying properties determined by their shear, twist and various Lie bracket relations, a family of Kähler metrics g' is constructed, defined on an open set in M, which
  coincides with M in many typical examples. Under certain conditions g and g' share various properties, such as a Killing vector field or a vector field with geodesic flow. The Ricci and scalar curvatures of g' are computed in some cases in terms of data associated to g. Many examples are described, including classical spacetimes in warped products, for instance de Sitter spacetime, as well as gravitational plane waves, Kerr (black hole) spacetime, and metrics for which g' is an SKR metric. For the latter an inverse ansatz is described, constructing g from the SKR metric.  This is joint work with Gideon Maschler.

• February 9, 2018
  Speaker:    Gabriel Katz (MIT)
  Title:    Holography and Scattering on Riemannian Manifolds with Boundary
  Abstract: For a given smooth compact manifold M​​, we introduce a massive class 𝒢(M)​​ of Riemannian metrics, which we call metrics of the gradient type. For such metrics g​​, the geodesic flow v^g​​ on the spherical tangent bundle SM → M​​ is traversing. Moreover, for every g ∈ 𝒢(M)​​, the geodesic scattering along the boundary ∂M​​ can be expressed in terms of the scattering map C_v^g: ∂₁⁺(SM) → ∂₁^-(SM)​​. It acts from a domain ∂₁⁺(SM)​​ in the boundary ∂(SM)​​ to the complementary domain ∂₁^-(SM)​​, both domains being diffeomorphic.  We prove that, for a boundary generic metric g ∈ 𝒢(M)​​ the map C_v^g​​ allows for a reconstruction of SM​​ and of the geodesic flow on it, up to a homeomorphism (often a diffeomorphism).
       Also, for such g​​,  the knowledge of the scattering map C_v^g​​ makes it possible to reconstruct the homology of M​, the Gromov simplicial semi-norm on it, and the fundamental group of M​​.
       We aim to understand the constraints on (M, g)​​, under which the scattering map allows for a reconstruction of M​​ and the metric g​​ on it. In particular, we consider a closed Riemannian n​​-manifold (N, g)​​ which is locally symmetric and of negative sectional curvature. Let M​​ is obtained from N​​ by removing an n ​​-ball such that the metric g|_M​​ is boundary generic and of the gradient type. Then we prove that  the scattering map C_v^g|M​​ makes it possible to recover N​​ and the metric g​​ on it.

• October 27, 2017
  Speaker:    Pierre Albin (University of Illinois Urbana-Champaign)
  Title:    The families index formula on stratified spaces
  Abstract: Stratified spaces arise naturally even when studying smooth objects, e.g., as algebraic varieties, orbit spaces of smooth group actions, and many moduli spaces. There has recently been a lot of
  activity developing analysis on these spaces and studying topological invariants such as the signature. I will report on joint work with Jesse Gell-Redman in which we study families of Dirac-type operators
  on stratified spaces and establish a formula for the Chern character of their index bundle.
  
  

• October 27, 2017
  Speaker:    Mark Kempton (Harvard)
  Title:    Curvature and Homology on Graphs
  Abstract: A popular theme in graph theory today is to take ideas and theorems from the "continuous world" (e.g. geometry of Riemannian manifolds) and reformulate them in the "discrete world" (e.g. on a graph).  In recent years, much work has been done defining notions of Ricci curvature for discrete graphs, as well as developing homology theories for graphs. In this talk, I will connect these two areas by proving a homology vanishing theorem for graphs with positive curvature.  This result is analogous to a classical theorem of Bochner on Riemannian manifolds.  The proof draws on several different areas of graph theory.

• October 13, 2017
  Speaker:    Maxim Braverman (Northeastern)
  Title:    Relative index theorem and relative heat kernel
  Abstract: I will formulate the Gromov-Lawson relative index theorem and discuss the heat kernel approach to its proof. Specifically, I will consider two complete Riemannian manifolds which are isometric outside of compact subsets and two Dirac-type operators  and  on these manifolds whose restriction to the non-compact parts are equal. I will discuss the properties of the relative heat operator . I will discuss the conditions under which this operator is of trace class and the trace gives the relative index of  and . My exposition will follow the papers of Donnelly and Bunke. Though no really new results will be presented, the point of view will be slightly different than that of the cited papers. Also the operators I consider are slightly more general than those considered by Donnelly and Bunke.

• October 6, 2017
  Speaker:    Pengshuai Shi (Northeastern)
  Title:    The Atiyah-Patodi-Singer index on manifolds with non-compact boundary
  Abstract: We study the index of the APS boundary value problem for a strongly Callias-type operator D on a complete Riemannian manifold M. We use this index to define the relative eta-invariant  of two strongly Callias-type operators A and A', which are equal outside of a compact set. Even though in our situation the eta-invariants of A and A' are not defined, the relative eta-invariant behaves as if it were the difference of the eta-invariants of A and A'. We also define the spectral flow of a family of such operators and use it compute the variation of the relative eta-invariant. (Joint work with Maxim Braverman)

• September 29, 2017
  Speaker:    Robert McOwen (Northeastern)
  Title:    The Heat Semigroup on Weighted Sobolev and Asymptotic Spaces
  Abstract: We consider the heat equation on Euclidean space with initial condition in certain weighted Sobolev spaces, or certain spaces of functions allowing asymptotic expansions as |x| → ∞ of any given order. In fact, we show that the Laplacian on such function spaces generates an analytic semigroup and we investigate its regularity properties.

• September 22, 2017
  Speaker:    Dan Li (Purdue)
  Title:    Index theory and K-theory of topological insulators
  Abstract: Topological insulators are new materials observed in nature that can be characterized by a Z/2-valued invariant.This topological Z/2 invariant can be understood as a mod 2 index theorem in KR-theory.  I will give some background and talk about the relevant index theory and K-theory. 

• January 13, 2017
  Speaker:    Yanli Song (Dartmouth)
  Title:   K-homological and index on non-compact manifolds
  Abstract: Equivariant indices have previously been defined in cases where either the group or the orbit space in question is compact. In this talk, I will discuss an equivariant index without assuming the group or the orbit space to be compact, which take values in K-homology and group C*-algebras. This allows us to generalize an index of deformed Dirac operators, defined for compact groups by Braverman. This is a joint work with Peter Hochs.

• January 20, 2017
  Speaker:    Thomas Kappeler (University of Zurich)
  Title:  On the wellposedness of integrable PDEs: a survey of new results for the KdV, KdV2, and mKdV equations
  Abstract: In form of a case study, I survey the ‘nonlinear Fourier‘ method to solve nonlinear dispersive equations such as the Korteweg-de Vries (KdV) equation or the nonlinear Schrodinger (NLS) equation. A key ingredient for describing the solutions are the frequencies, associated to such type of equations. A novel approach of representing them allows to extend the solution map of such equations to spaces of low regularity and to study its regularity properties. Potential applications include results for stochastic versions of the evolution equations considered.
  This is joint work with Jan Molnar.

• January 27, 2017
  Speaker:    Semyon Dyatlov (MIT)
  Title:  Dynamical zeta functions and topology for negatively curved surfaces
  Abstract:  For a negatively curved compact Riemannian manifold (or more generally, for an Anosov flow), the Ruelle zeta function is defined by
  
  
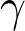
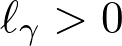
  where the product is taken over all primitive closed geodesics  with  denoting their length.  Remarkably, this zeta function continues meromorphically to all of .
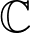
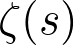
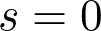
        Using recent advances in the study of resonances for Anosov flows and simple arguments from microlocal analysis, we prove that for an orientable negatively curved surface, the order of vanishing of  at  is given by the absolute value of the Euler characteristic. In constant curvature this follows from the Selberg trace formula and this is the first result of this kind for manifolds which are not locally symmetric. This talk is based on joint work with Maciej Zworski.
  .

• February 3, 2017
  Speaker:    Jonathan Weitsman (Northeastern)
  Title:  TBA
  Abstract: TBA.

• February 10, 2017
  Speaker:    Boris Khesin (U. Toronto)
  Title:  Invariants of functions on symplectic surfaces and ideal hydrodynamics
  Abstract: We describe a classification of simple Morse functions on symplectic surfaces with respect to actions of symplectomorphism groups. We also classify generic coadjoint orbits and Casimirs for such groups. This gives an answer to V.Arnold's problem on describing all invariants of generic isovorticed fields for the 2D ideal incompressible fluids. For this we introduce a notion of anti-derivatives on a measured Reeb graph and outline their properties. This is a joint work with Anton Izosimov and Mehdi Mousavi.

• April 7, 2017
  Speaker:    Erik van Erp (Dartmouth)
  Title:  TBA
  Abstract: TBA.

• October 28, 2016
  Speaker:    Pengshuai Shi (Northeastern)
  Title:  The index of Callias-type operators with Atiyah-Patodi-Singer boundary condition
  Abstract: We compute  the index of a Callias-type operator on a complete Riemannian manifold with a compact boundary with the Atiyah-Patodi-Singer boundary conditions  in terms of indexes of induced operators on a compact manifold.
  

• November 4, 2016
  Speaker:    Yernat Assylbekov (Northeastern)
  Title:  Inversion formulas and range characterizations for the attenuated geodesic ray transform
  Abstract: We present two range characterizations for the attenuated geodesic X-ray transform defined on pairs of functions and one-forms on simple surfaces. Such characterizations are based on first isolating the range over sums of functions and one-forms, then separating each sub-range in two ways, first by implicit conditions, second by deriving new inversion formulas for sums of functions and one-forms. (joint work with Francois Monard and Gunther Uhlmann)
  

• November 18, 2016
  Speaker:    Peter Hochs (University of Adelaide)
  Title:  TBA
  Abstract: TBA

• April 21, 2016, 12 PM at 544NI (Note  the unusual room)
  Speaker:    Anton Izosimov (U. Toronto) Note special date and time
  Title:  Coadjoint orbits and steady solutions for the 2D Euler equation
  Abstract: The motion of an ideal fluid on a 2D surface is described by the incompressible Euler equation, which can be regarded as a Hamiltonian system on coadjoint orbits of the symplectic diffeomorphisms group. Using a combinatorial description of these orbits in terms of graphs with some additional structures, we give a characterization of coadjoint orbits which may admit steady solutions of the Euler equation (steady fluid flows). It turns out that when the genus of the surface is at least one, most coadjoint orbits do not admit steady fluid flows, while the set of orbits admitting such flows is a convex polytope.
          (This is a joint work with B.Khesin.)

• April 8, 2016
  Speaker:    Simone Cecchini (Northeastern)
  Title:  Callias-type operators in von Neumann algebras
  Abstract: We study differential operators on complete Riemannian manifolds which act on sections of a bundle of finite type modules over a von Neumann algebra with a trace. We prove a relative index and a Callias-type index theorems for von Neumann indexes of such operators. We apply these results to obtain a version of Atiyah's L²-index theorem, which states that the index of a Callias-type operator on a non-compact manifold M is equal to the Γ-index of its lift to a Galois cover of M.  We also prove the cobordism invariance of the index of Callias-type operators. In particular, we give a new proof of the cobordism invariance of the von Neumann index of operators on compact manifolds.
   (Joint work with Maxim Braverman).

• April 1, 2016
  Speaker:    Jared Speck (MIT)
  Title:  An overview of recent progress on shock formation in three spatial dimensions
  Abstract: Classical solutions to many quasilinear hyperbolic PDEs without special structure are expected to often form shocks, which are singularities where the solution remains bounded but its derivatives blow-up. Although many such results have been proved in one spatial dimension, there are very few rigorous results in higher dimensions. In this talk, I will provide an overview of recent progress on the formation of shocks in the case of three spatial dimensions. I will start by describing prior contributions from many researchers including F. John, S. Alinhac, and especially D. Christodoulou, whose remarkable 2007 work exhibited an open set of small-data solutions to the relativistic Euler equations that form shocks in vorticity-free regions. I will then describe some results from my recent monograph, in which I show that for two important classes of wave equations in three spatial dimensions, a sufficient condition for small-data shock-formation is the failure of S. Klainerman’s null condition. The results provide a sharp converse to the well-known result, due separately to Christodoulou and Klainerman, that small-data global existence holds if the null condition is satisfied. I will highlight some of the main ideas behind the analysis including the critical role played by geometric decompositions based on true characteristic hypersurfaces. The geometric framework allows for a complete description of the shape of the boundary of the region of classical existence and the mechanism that drives the singularity formation. Some aspects of this work are joint with G. Holzegel, S. Klainerman, and W. Wong.

• March 25, 2016
  Speaker:    Bob McOwen (Northeastern)
  Title:  Differentiability of Solutions to the Neumann Problem with Low-Regularity Data via Dynamical Systems
  Abstract: We obtain conditions for the differentiability of weak solutions for a second-order uniformly elliptic equation in divergence form with a homogeneous co-normal boundary condition. The modulus of continuity for the coefficients is assumed to satisfy the square-Dini condition and the boundary is assumed to be differentiable with derivatives also having this modulus of continuity. Additional conditions for the solution to be Lipschitz continuous or differentiable at a point on the boundary depend upon the stability of a dynamical system that is derived from the coefficients of the elliptic equation.

• March 18, 2016
  Speaker:    Chenjie Fan (MIT)
  Title:  Log-log blow up solutions of NLS at exactly m points
  Abstract: We will first introduce the log-log blow up solutions to NLS which have been studied by Merle and Raphael and many other authors. Then, we will illustrate our construction about  certain solutions to NLS, which blow up at $m$ prescribed points according to log-log law. The idea is to use bootstrap to show the $m$ bubbles can be decoupled, and then use soft topological argument to balance different bubbles, making them blow up simultaneously at the prescribed points.

• March 4, 2016
  Speaker:    Boris Hanin (MIT)
  Title:   Scaling Limit of Spectral Projector for the Laplacian on a Compact Riemannian Manifold
  Abstract: Let (M,g) be a compact smooth Riemannian manifold. I will give some new off-diagonal estimates for the remainder in the pointwise Weyl Law. A corollary is that, when rescaled around a non self-focal point, the kernel of the spectral projector of the Laplacian onto the frequency interval (lambda,lambda+1] has a universal scaling limit as lambda goes to infinity (depending only on the dimension of M). This is joint work with Y. Canzani.

• February 26 , 2016
  Speaker:    Raphael Ponge (Seoul National University and McGill University)
  Title:  Nocommutative geometry, equivariant cohomology, and conformal geometry
  Abstract: The aim of this talk is to present applications of noncommutative geometry techniques to conformal differential geometry. Three main results should be covered. The first result is a reformulation of the local index formula of Atiyah-Singer in conformal geometry, i.e., in the setting of the action of an arbitrary group of conformal-diffeomorphisms. The second result is the construction of new conformal invariants out of equivariant characteristic classes. The third result is a version in conformal geometry of the Vafa-Witten inequality for eigenvalues of Dirac operators. This is based on joint work with Hang Wang (University of Adelaide, Australia). 

• November 6, 2015
  Speaker:    Pedram Hekmati  (IMPA, Brazil)
  Title:  Topological T-duality and Hodgkin's theorem
  Abstract: A famous problem in topology, first solved by Hodgkin in 1967, is to determine the K-theory of compact simply-connected Lie groups. Hodgkin's original proof was extremely technical, motivating the discovery of a number of simpler proofs. In this talk I will present a new, surprisingly simple proof of Hodgkin's theorem using topological T-duality, an idea that originated in physics. This is based on joint work with David Baraglia.

• October 16, 2015
  Speaker:    Seckin Demirbas  (Northeastern University)
  Title:  Gibbs' measure and almost sure global well-posedness for one dimensional periodic fractional Schrödinger equation
  Abstract: In this talk we will present recent local and global well-posedness results on the one dimensional periodic fractional Schr\"odinger equation. We will also talk about construction of Gibbs' measures on certain Sobolev spaces and how we can prove almost sure global well-posedness using this construction.

• October 9, 2015
  Speaker:    Long Jin  (Harvard)
  Title:  A local trace formula for Anosov flows
  Abstract: In this talk, we present a local trace formula for Anosov flows on compact manifolds which relates Pollicott-Ruelle resonances to the periods of closed orbits. As an application, we show a weak lower bound for the counting function for resonances in a strip and thus the infinitude of the resonances. This is joint work with Maciej Zworski and Frederic Naud.

• October 2, 2015
  Speaker:     Gabriel Katz 
  Title:  The Holography Theorem
  Abstract: Let  be a smooth nonsingular gradient-like vector field on a smooth compact manifold  with boundary. Let  denote the oriented 1-dimensional foliation produced by the -flow.
      The general question that I am trying to answer is: What kind of residual structure on the boundary  will allow for a reconstruction of  and of the foliation ? 
  If such a reconstruction of the pair  is possible, the structure on the boundary deserves the name "holographic".
      The boundary  consists of two parts: , where the vector field  is pointing inwards of , and , where the field is pointing outwards.   For each point , consider the "closest" point , where the -trajectory through  exits  or is tangent to its boundary. Thus, we get a map
  
  
  which we call "the causality map" ( is only semi-continuous). It turns out that the causality map  is an example of the desired holographic data.
      In the talk, I will explain the following {\bf Holography Theorem}
   For a generic gradient-like vector field  on , the smooth type of  and the un-parameterized dynamics of the -flow can be reconstructed from the causality map .
  
  
  The Holography Theorem has numerous applications to the smooth dynamics of vector flows of non-gradient types as well.  These applications include the classical inverse scattering problems, the geodesic flows, and the geodesic billiards on Riemannian manifolds with boundary.
  
  

• September 18, 2015
  Speaker:     Karsten Fritzsch (University College London)
  Title:  Layer Potential Operators for Two Touching Domains in Rⁿ
  Abstract: So far, no special framework for the study of layer potential operators (or similar operators) on manifolds with corners has been developed even though both approaches, the method of layer potentials and the calculus of conormal distributions on manifolds with corners, have been proven to be very successful.
     In this talk, I will demonstrate in a certain singular case that the geometric viewpoint of singular geometric analysis leads to a feasible approach to the method of layer potentials: I will show a way towards solving the (exterior) Dirichlet and Neumann problems for Laplace's equation on two touching domains in Rⁿ in spaces of functions having certain (though very general) asymptotics. Using the Push-Forward Theorem, on the one hand I will show that the relations between the layer potential operators and their boundary counterparts continue to hold in the singular setting, and on the other hand establish mapping properties of the layer potential operators between spaces of functions with asymptotics. We can improve these by using a local splitting of certain fibrations which arise when applying the Push-Forward Theorem.
     In the first part of the talk, I will briefly introduce some background material, in particular the method of layer potentials, polyhomogeneity and the Push-Forward Theorem, and the b- and φ-calculi of pseudodifferential operators. If time permits, I will end the talk by sketching the connection to the plasmonic eigenvalue problem on touching domains.
  
  

Comments to: