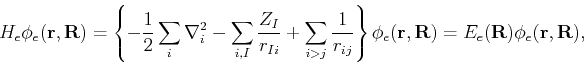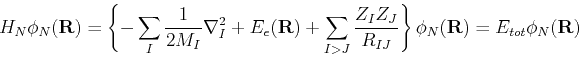The Born-Oppenheimer Approximation is the assumption that the electronic motion and the nuclear motion in molecules can be separated. It leads to a molecular wave function in terms of electron positions and nuclear positions.
This involves the following assumptions:
![]() The electronic wavefunction depends upon the nuclear positions but not upon their velocities, i.e., the nuclear motion is so much slower than electron motion that they can be considered to be fixed.
The electronic wavefunction depends upon the nuclear positions but not upon their velocities, i.e., the nuclear motion is so much slower than electron motion that they can be considered to be fixed.
![]() The nuclear motion (e.g., rotation, vibration) sees a smeared out potential from the speedy electrons.
The nuclear motion (e.g., rotation, vibration) sees a smeared out potential from the speedy electrons.
We know that if a Hamiltonian is separable into two or more terms, then the total eigenfunctions are products of the individual eigenfunctions of the separated Hamiltonian terms, and the total eigenvalues are sums of individual eigenvalues of the separated Hamiltonian terms.
Consider, for example, a Hamiltonian which is separable into two terms, one involving coordinate ![]() and the other involving coordinate
and the other involving coordinate ![]() .
.
If we assume that the total wavefunction can be written in the form
![]() , where
, where ![]() and
and ![]() are eigenfunctions of
are eigenfunctions of ![]() and
and ![]() with eigenvalues
with eigenvalues ![]() and
and ![]() , then
, then
| (54) | |||
| (55) | |||
| (56) | |||
| (57) | |||
| (58) |
Going back to our original problem, Eq.(3),
, we would start by seeking the eigenfunctions and eigenvalues of this Hamiltonian, which will be given by solution of the time-independent Schrödinger equation
We first invoke the Born-Oppenheimer approximation by recognizing that, in a dynamical sense, there is a strong separation of time scales between the electronic and nuclear motion, since the electrons are lighter than the nuclei by three orders of magnitude. This can be exploited by assuming a quasi-separable ansatz of the form
After these considerations,
![]() can be neglected since
can be neglected since ![]() is smaller than
is smaller than ![]() by a factor of
by a factor of ![]() . Thus for a fixed nuclear configuration, we have
. Thus for a fixed nuclear configuration, we have
| (59) | |||
| (60) |
We now consider again the original Hamiltonian (3). If we insert a wavefunction of the form
![]() , we obtain
, we obtain
Using these facts, along with the electronic Schrdöinger equation,
| (63) |
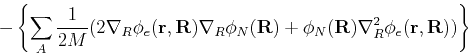 |
(64) |
| (65) |
We must now estimate the magnitude of the last term in brackets. A typical contribution has the form
![]() , but
, but
![]() is of the same order as
is of the same order as
![]() since the derivatives operate over approximately the same dimensions. The latter is
since the derivatives operate over approximately the same dimensions. The latter is
![]() , with
, with ![]() the momentum of an electron. Therefore
the momentum of an electron. Therefore
![]() . Since
. Since
![]() , the term in brackets can be dropped, giving
, the term in brackets can be dropped, giving
To summarize, the large difference in the relative masses of the electrons and nuclei allows us to approximately separate the wavefunction as a product of nuclear and electronic terms. The electronic wavefucntion
![]() is solved for a given set of nuclear coordinates,
is solved for a given set of nuclear coordinates,