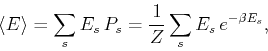The Canonical Ensemble

Most physical systems are not isolated, bu exchange energy with the environment. Since the system is very small compared to the environment, we consider that the environment acts effectively as a heat reservoir or heat bath at a fixed temperature $T$. If a small system is put in thermal contact with the heat bath, it will reach thermal equilibrium exchanging energy until the system attains the temperature of the bath.

Imagine an infinitely large number of mental copies of the system and the heat bath. The probability $P_s$ that the system is found in a microstate $s$ with energy $s$ is given by:

$$P_s=\frac{1}{Z}e^{-E_s/k_BT},$$ (274)

where $Z$ is the normalization constant. This corresponds to the canonical ensemble. Since $\sum P_s = 1$, we have

$$Z=\sum_s{e^{-E_s/k_BT}},$$ (275)

where the sum is over all the possible microstates of the system. This equation defines the ``partition function'' of the system.

We can use (276) to obtain the ensemble average of physical quantities of interest. For instance, the mean energy is given by:

$$\langle E \rangle = \sum_s E_s P_s=\frac{1}{Z}\sum_s{E_s e^{-\beta E_s}},$$

with $\beta=1/k_BT$.