


Next: Exercise 10.2: Importance of
Up: Monte Carlo error analysis
Previous: Monte Carlo error analysis
- Write a program that implements the ``hit and miss'' Monte
Carlo integration
algorithm. Find the estimate
 for the integral of
for the integral of
as a function of 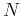 , in the interval
, in the interval  . Choose
. Choose 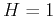 , and sample
only the
, and sample
only the  -dependent part
-dependent part 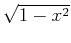 , and multiply the result by 4.
Calculate the difference between
, and multiply the result by 4.
Calculate the difference between  and the exact result
and the exact result 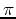 . This
difference is a measure of the error associated with the Monte Carlo
estimate. Make a log-log plot of the error as a function of
. This
difference is a measure of the error associated with the Monte Carlo
estimate. Make a log-log plot of the error as a function of 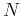 . What is
the approximate functional deppendece of the error on
. What is
the approximate functional deppendece of the error on 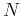 for large
for large 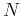 ?
?
- Estimate the integral of
 using the simple Monte Carlo
integration by averaging over
using the simple Monte Carlo
integration by averaging over 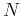 points, using
(270), and compute the error as a function of
points, using
(270), and compute the error as a function of 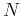 , for
, for 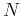 upt to 10,000. Determine the approximate functional deppendence of the
error on
upt to 10,000. Determine the approximate functional deppendence of the
error on 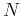 for large
for large 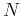 . How many trials are necessary to determine
. How many trials are necessary to determine
 to two decimal places?
to two decimal places?
- Perform 10 measurements
 , with
, with 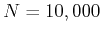 using different
random sequences. Show in a table the values of
using different
random sequences. Show in a table the values of  and
and 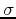 according to (270) and (271). Use
(272) to estimate the standard deviation of the means, and
compare to the values obtained from (273) using the 100,000
values.
according to (270) and (271). Use
(272) to estimate the standard deviation of the means, and
compare to the values obtained from (273) using the 100,000
values.
- To verify that your result for the error is independent of the
number of sets you used to divide your data, repeat the previous item
grouping your results in 20 groups of 5,000 points each.



Next: Exercise 10.2: Importance of
Up: Monte Carlo error analysis
Previous: Monte Carlo error analysis
Adrian E. Feiguin
2009-11-04