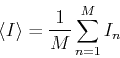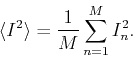Next: Exercise 10.1: One dimensional
Up: Monte Carlo integration
Previous: Simple Monte Carlo integration
The Monte Carlo method clearly yields approximate results. The accuracy
deppends on the number of values 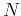 that we use for the average. A
possible measure of the error is the ``variance''
that we use for the average. A
possible measure of the error is the ``variance''  defined
by:
defined
by:
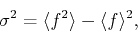 |
(269) |
where
and
The ``standard deviation'' is 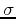 . However, we should expect that
the error decreases with the number of points
. However, we should expect that
the error decreases with the number of points 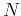 , and the quantity
, and the quantity
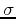 defines by (271) does not. Hence, this cannot be a
good measure of the error.
defines by (271) does not. Hence, this cannot be a
good measure of the error.
Imagine that we perform several measurements of the integral, each of
them yielding a result  . Thes values have been obtained
with different sequences of
. Thes values have been obtained
with different sequences of 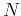 random numbers. According to the central
limit theorem,
these values whould be normally dstributed around a mean
random numbers. According to the central
limit theorem,
these values whould be normally dstributed around a mean
 . Suppouse that we have a set of
. Suppouse that we have a set of 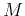 of such measurements
of such measurements
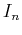 . A convenient measure of the differences of these measurements is
the ``standard deviation of the means''
. A convenient measure of the differences of these measurements is
the ``standard deviation of the means'' 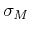 :
:
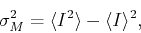 |
(270) |
where
and
Although 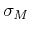 gives us an estimate of the actual error, making
additional meaurements is not practical. instead, it can be proven that
gives us an estimate of the actual error, making
additional meaurements is not practical. instead, it can be proven that
 |
(271) |
This relation becomes exact in the limit of a very large number of
measurements. Note that this expression implies that the error decreases
withthe squere root of the number of trials, meaning that if we want to
reduce the error by a factor 10, we need 100 times more points for the
average.
Subsections



Next: Exercise 10.1: One dimensional
Up: Monte Carlo integration
Previous: Simple Monte Carlo integration
Adrian E. Feiguin
2009-11-04
![]() that we use for the average. A
possible measure of the error is the ``variance''
that we use for the average. A
possible measure of the error is the ``variance'' ![]() defined
by:
defined
by:
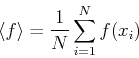

![]() . Thes values have been obtained
with different sequences of
. Thes values have been obtained
with different sequences of ![]() random numbers. According to the central
limit theorem,
these values whould be normally dstributed around a mean
random numbers. According to the central
limit theorem,
these values whould be normally dstributed around a mean
![]() . Suppouse that we have a set of
. Suppouse that we have a set of ![]() of such measurements
of such measurements
![]() . A convenient measure of the differences of these measurements is
the ``standard deviation of the means''
. A convenient measure of the differences of these measurements is
the ``standard deviation of the means'' ![]() :
: