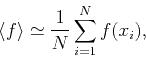More generaly, imagine a rectangle of height ![]() in the
integration interval
in the
integration interval ![]() ,
such that the function
,
such that the function ![]() is within its boundaries. Compute
is within its boundaries. Compute ![]() pairs
of random numbers
pairs
of random numbers ![]() such that they are uniformly distributed
inside this rectangle. The fraction of points that fall within the area
contained below
such that they are uniformly distributed
inside this rectangle. The fraction of points that fall within the area
contained below ![]() , i. e., that satisfy
, i. e., that satisfy
![]() is an
estimate of the ratio o fthe integral of
is an
estimate of the ratio o fthe integral of ![]() and the area of the
rectangle. Hence, the estimate of the integral will be given by:
and the area of the
rectangle. Hence, the estimate of the integral will be given by:
Another Monte Carlo procedure is based on the definition: