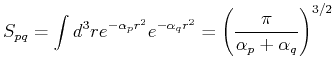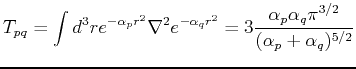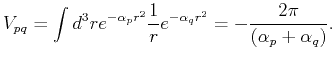Next: Exercise 2.2: Hydrogen atom
Up: Examples of linear variational
Previous: Exercise 2.1: Infinite potential
One example of the variational method would be using the Gaussian function
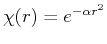 as a trial function for the hydrogen atom ground state. This problem could be solved by the variational method by obtaining the energy of
as a trial function for the hydrogen atom ground state. This problem could be solved by the variational method by obtaining the energy of 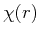 as a function of the variational parameter
as a function of the variational parameter  , and then minimizing
, and then minimizing  to find the optimum value
to find the optimum value 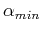 . The variational theorem's approximate wavefunction and energy for the hydrogen atom would then be
. The variational theorem's approximate wavefunction and energy for the hydrogen atom would then be
 and
and
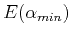 .
.
This is a one electron problem, so we do not have to worry about electron-electron interactions, or antisymmetrization of the wave function.
The Schrödinger's equation reads:
![\begin{displaymath}
\left[ -\frac{\hbar^2}{2m}\nabla^2 - \frac{e^2}{4\pi\epsilon_0}\frac{1}{r} \right] \psi(x) = E \psi(x)
\end{displaymath}](img82.png) |
(36) |
where the second term is the Coulomb interaction with the positive nucleus (remember, this is a charged particle in a central potential). The mass 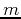 is the reduced mass of the proton-electron system, which is approximately equal to the electron mass. The ground state has energy
is the reduced mass of the proton-electron system, which is approximately equal to the electron mass. The ground state has energy
 |
(37) |
and the wave function is given by
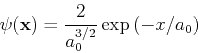 |
(38) |
where  is Bohr's radius
is Bohr's radius
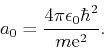 |
(39) |
It is convenient to use units such that equations take on a simpler form. These are the so-called standard units in electronic structure: the unit of distance is Bohr's radius, masses are expressed in units of the electon mass  , and charge in units of the electron charge e. The energy is finally given in ``hartrees'', equal to
, and charge in units of the electron charge e. The energy is finally given in ``hartrees'', equal to
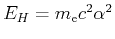 (where
(where  is the fine structure constant). In these units the Schrödinger equation for the hydrogen atom assumes the following simpler form:
is the fine structure constant). In these units the Schrödinger equation for the hydrogen atom assumes the following simpler form:
![\begin{displaymath}
\left[ -\frac{1}{2}\nabla^2 - \frac{1}{r} \right] \psi(x) = E \psi(x).
\end{displaymath}](img90.png) |
(40) |
To approximate the ground state energy and wave function of the hydrogen atom in a linear variational procedure, we will use Gaussian basis functions. For the ground state, we only need angular momentum  wave functions (
wave functions ( -orbitals), which have the form:
-orbitals), which have the form:
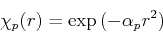 |
(41) |
centered on the nucleus (whis is thus placed at the origin). We have to specify the values of the exponents 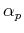 , which are our variational parameters. Optimal values of these exponents have been previously found by other means, and
in our case, we will keep these values fixed:
, which are our variational parameters. Optimal values of these exponents have been previously found by other means, and
in our case, we will keep these values fixed:
If the program works correctly, it should shield a value of the energy close to the exact results 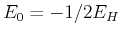 .
.
It remains to determine the coefficients of the linear expansion, by solving the generalized eigenvalue problem, as we did in the previous example.
The matrix elements of
the overlap matrix 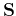 , the kinetic energy matrix
, the kinetic energy matrix 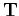 , and the Coulomb interaction
, and the Coulomb interaction  are given by:
are given by:
Using these expressions, one can fill the overlap and Hamiltonian matrices and solve the problem numerically.



Next: Exercise 2.2: Hydrogen atom
Up: Examples of linear variational
Previous: Exercise 2.1: Infinite potential
Adrian E. Feiguin
2009-11-04
![]() as a trial function for the hydrogen atom ground state. This problem could be solved by the variational method by obtaining the energy of
as a trial function for the hydrogen atom ground state. This problem could be solved by the variational method by obtaining the energy of ![]() as a function of the variational parameter
as a function of the variational parameter ![]() , and then minimizing
, and then minimizing ![]() to find the optimum value
to find the optimum value ![]() . The variational theorem's approximate wavefunction and energy for the hydrogen atom would then be
. The variational theorem's approximate wavefunction and energy for the hydrogen atom would then be
![]() and
and
![]() .
.
![\begin{displaymath}
\left[ -\frac{\hbar^2}{2m}\nabla^2 - \frac{e^2}{4\pi\epsilon_0}\frac{1}{r} \right] \psi(x) = E \psi(x)
\end{displaymath}](img82.png)

![]() wave functions (
wave functions (![]() -orbitals), which have the form:
-orbitals), which have the form:
![]() , the kinetic energy matrix
, the kinetic energy matrix ![]() , and the Coulomb interaction
, and the Coulomb interaction ![]() are given by:
are given by: