 |
(243) |
We have defined our APW as:
If an eigenfunction would be discontinuous, its kinetic energy would not be well-defined.
Such a situation can therefore never happen, and we have to require that the plane wave
outside the sphere matches the function inside the sphere over the complete surface of the
sphere (in value, not in slope). That seems a weird thing to do: a plane wave is oscillating and
has a unique direction built in, how can it match another function based on spherical harmonics
over the entire surface of a sphere? To see how this is possible, we expand the plane wave in
spherical harmonics:
 |
(244) |
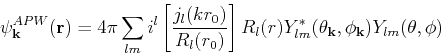 |
(245) |
The APW function is no a solution to the Scrödinger equation, but they are appropriate for expanding the actual wave function.
The APW method tries to approximate the correct solution to the crystal by a superposition of APW's, all with the same energy. For any reciprocal lattice vector ![]() , the APW satisfies the Bloch condition with wave vector k, but for the entire wavefunctioon to be of the Bloch form we need the expansion of
, the APW satisfies the Bloch condition with wave vector k, but for the entire wavefunctioon to be of the Bloch form we need the expansion of
![]()
| (246) |
The hope is that we swill need only a small number of APW's to approximate the full Schrödinger euqation in the interstitial region and at the boundary. In practice, as many as a several hundreeds can be used. By the time we do this, the energy does not change much, as more APW's are added, and we achieve convergence.
All the APW have to be evaluated at the same energy. The coefficients are given, again, by solving the generalized eigenvalue equation
| (247) |
The most remarkable aspect of this equation is, that even though is looks like an ordinary eigenvalue problem, the marix elements depend on energy! To solve the problem it is convenient to work a fixed energy, and look for the ![]() 's at which the following secular expresion is satisfied:
's at which the following secular expresion is satisfied:
| (248) |