


Next: Exercise 2.1: Infinite potential
Up: Examples of linear variational
Previous: Examples of linear variational
The potential well with inifinite barriers is defined:
 |
(28) |
and it forces the wave function to vanish at the boundaries of the well at  . The exact solutioon for this problems is known and treated in introductory quantum mechanics courses. Here we discuss a linear variational approach to be compared with the exact solution. We take
. The exact solutioon for this problems is known and treated in introductory quantum mechanics courses. Here we discuss a linear variational approach to be compared with the exact solution. We take 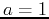 and use natural units such that
and use natural units such that 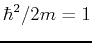 .
.
As basis functions we take simple polynomials that vanish on the boundaries of the well:
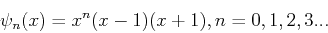 |
(29) |
The reason for choosing this particular form of basis functions is that the relevant matrix elements can easily be calculated analytically. We start we the overlap matrix:
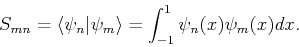 |
(30) |
Working out the integrals, one obtains
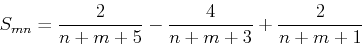 |
(31) |
for  even, and zero otherwise.
even, and zero otherwise.
We can also calculate the Hamiltonian matrix elements:
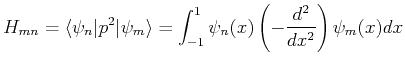 |
|
|
(32) |
![$\displaystyle = -8 \left[ \frac{1-m-n-2mn}{(m+n+3)(m+n+1)(m+n-1)} \right]$](img67.png) |
|
|
(33) |
for 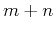 even, and zero otherwise.
even, and zero otherwise.



Next: Exercise 2.1: Infinite potential
Up: Examples of linear variational
Previous: Examples of linear variational
Adrian E. Feiguin
2009-11-04


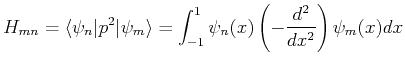
![$\displaystyle = -8 \left[ \frac{1-m-n-2mn}{(m+n+3)(m+n+1)(m+n-1)} \right]$](img67.png)