


Next: Solution to the Kohn-Sham
Up: Density Functional Theory
Previous: Limitations
Let us define a new quantity
 |
(162) |
We can easily see that the exchange correlation energy may be written
![\begin{displaymath}
E_{xc}[n] = \frac{1}{2} \int d^3r_1 d^3r_2 n({\bf r}_1)n_{xc}({\bf r}_1,{\bf r}_2) \frac{1}{r_{12}}.
\end{displaymath}](img383.png) |
(163) |
This is the Coulomb interaction of each electron with a charge distribution 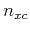 , whcih can be interpreted as a conditional density. This conditional density vanished as the distance between the particles goes to zero, and may be interpreted as a ``hole'' surrounding each particle, and it is named exchange correlation hole.
We can see that this hole orrespond to a unit of charge by anotehr sum-rule:
, whcih can be interpreted as a conditional density. This conditional density vanished as the distance between the particles goes to zero, and may be interpreted as a ``hole'' surrounding each particle, and it is named exchange correlation hole.
We can see that this hole orrespond to a unit of charge by anotehr sum-rule:
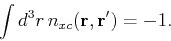 |
(164) |
We can consider  as a normalizationo factor and define the radius of the exchange hole as:
as a normalizationo factor and define the radius of the exchange hole as:
 |
(165) |
Thsi leads to
![\begin{displaymath}
E_{xc}[n] = -\frac{1}{2}\int d^3r n({\bf r}) \left \langle \frac{1}{R} \right \rangle
\end{displaymath}](img388.png) |
(166) |
showing that, privided that the sum-rule is satisfied, the exchange-correlation energy depends only weakly on the details of 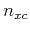 . Thsi means that even if our approximation is nto able to describe the detailed spatial shape of the hole, as long as the sum-rule is fulfuilled, the errors are small, and LDA will produce good results.
. Thsi means that even if our approximation is nto able to describe the detailed spatial shape of the hole, as long as the sum-rule is fulfuilled, the errors are small, and LDA will produce good results.



Next: Solution to the Kohn-Sham
Up: Density Functional Theory
Previous: Limitations
Adrian E. Feiguin
2009-11-04
![]() as a normalizationo factor and define the radius of the exchange hole as:
as a normalizationo factor and define the radius of the exchange hole as:
