


Next: The local density approximation
Up: DFT formalism and derivation
Previous: Non-interacting case
The energy-functional for a many-body system with the electronic interaction taken into account reads
![\begin{displaymath}
E\left[n({\bf r}) \right] = T\left[n({\bf r}) \right] + \in...
...\frac{1}{\vert{\bf r} - {\bf r}'\vert} n({\bf r}) + E_{xc}[n],
\end{displaymath}](img365.png) |
(154) |
where the last term, the exchange correlation energy, contains by definition all the contributions not taken into account by the first three terms. We have made no approximation, we simply moved all the unknown correlations into 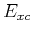 , whcih depends on the density instead of the explicit form of the wavefunction.
Varying this equation with respet to the density we obtain:
, whcih depends on the density instead of the explicit form of the wavefunction.
Varying this equation with respet to the density we obtain:
![\begin{displaymath}
\frac{\delta T[n]}{\delta n({\bf r}) } + \frac{\delta E_{xc}...
...frac{1}{\vert{\bf r}-{\bf r}'\vert} + V_{ext}({\bf r}) = \mu ,
\end{displaymath}](img367.png) |
(155) |
This equation has the same form as (152) with the difference that the potential has been replaced by an effective one:
![\begin{displaymath}
V_{eff}({\bf r}) = V_{ext}({\bf r}) + \frac{\delta E_{xc}[n]...
...}+\int d^3r' n({\bf r}') \frac{1}{\vert{\bf r}-{\bf r}'\vert}.
\end{displaymath}](img368.png) |
(156) |
The corresponding Schrödinger equation for the one-particle wavefunctions is
![\begin{displaymath}
\left[-\frac{1}{2}\nabla ^2 + V_{eff}({\bf r}) \right] \psi_k({\bf r}) = \epsilon_k \psi_k({\bf r}).
\end{displaymath}](img369.png) |
(157) |
Same as for Hartree-Fock, summing over all the eigenvalues leads to overestimating the Hartree energy by a factor of 2, and further difference in the exchange correlation energy. The corresponding expression for the ground-state energy is:
![\begin{displaymath}
E = \sum_{k=1}^N \epsilon_k - \frac{1}{2} \int d^3r d^3r' n(...
...\bf r}') + E_{xc}[n] - \int d^3r V_{xc}[n({\bf r})]n({\bf r}).
\end{displaymath}](img370.png) |
(158) |
where
![\begin{displaymath}
V_{xc}= \frac{\delta E_{xc}[n]}{\delta n({\bf r}) }
\end{displaymath}](img371.png) |
(159) |
These are the so-called Kohn and Sham equations.
From here we obtain the kinetic term as:
![\begin{displaymath}
T[n] = \sum_{i=1}^N \epsilon_i - \int n({\bf r}) V_{eff}({\bf r}) d^3r
\end{displaymath}](img372.png) |
(160) |
and the density
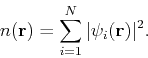 |
(161) |
It is very important to be careful when considering the individual eigenvalues 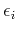 . In general they cannot be associated to any excitation energy, which would be a nive and natural interpretation.
. In general they cannot be associated to any excitation energy, which would be a nive and natural interpretation.
The main problem with the Kohn-Sham equations is that we do not know the exact expression for the exchange functional, we can only use some properly chosen functionals based on educated guesses, as we are going to see next.



Next: The local density approximation
Up: DFT formalism and derivation
Previous: Non-interacting case
Adrian E. Feiguin
2009-11-04
![\begin{displaymath}
E\left[n({\bf r}) \right] = T\left[n({\bf r}) \right] + \in...
...\frac{1}{\vert{\bf r} - {\bf r}'\vert} n({\bf r}) + E_{xc}[n],
\end{displaymath}](img365.png)
![\begin{displaymath}
E\left[n({\bf r}) \right] = T\left[n({\bf r}) \right] + \in...
...\frac{1}{\vert{\bf r} - {\bf r}'\vert} n({\bf r}) + E_{xc}[n],
\end{displaymath}](img365.png)
![\begin{displaymath}
\frac{\delta T[n]}{\delta n({\bf r}) } + \frac{\delta E_{xc}...
...frac{1}{\vert{\bf r}-{\bf r}'\vert} + V_{ext}({\bf r}) = \mu ,
\end{displaymath}](img367.png)
![\begin{displaymath}
V_{eff}({\bf r}) = V_{ext}({\bf r}) + \frac{\delta E_{xc}[n]...
...}+\int d^3r' n({\bf r}') \frac{1}{\vert{\bf r}-{\bf r}'\vert}.
\end{displaymath}](img368.png)
![\begin{displaymath}
E = \sum_{k=1}^N \epsilon_k - \frac{1}{2} \int d^3r d^3r' n(...
...\bf r}') + E_{xc}[n] - \int d^3r V_{xc}[n({\bf r})]n({\bf r}).
\end{displaymath}](img370.png)
![\begin{displaymath}
V_{xc}= \frac{\delta E_{xc}[n]}{\delta n({\bf r}) }
\end{displaymath}](img371.png)
![\begin{displaymath}
T[n] = \sum_{i=1}^N \epsilon_i - \int n({\bf r}) V_{eff}({\bf r}) d^3r
\end{displaymath}](img372.png)
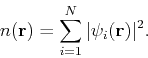
![]() . In general they cannot be associated to any excitation energy, which would be a nive and natural interpretation.
. In general they cannot be associated to any excitation energy, which would be a nive and natural interpretation.