Non-interacting case

Consider the separation of the Hamiltonian as

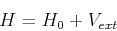$$H = H_0 + V_{ext}$$ (147)

where 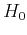$H_0$ corresponds to the non-interacting homogeneouos electron gas.

Then the functional reads:

$$E[n] = F[n] + \int d^3 r n({\bf r}) V_{\hbox{{ext}}}({\bf r})$$ (148)

with

$$F[n] = \min_{\Psi\vert n} \langle \Psi \vert H_0 \vert \Psi \rangle$$ (149)

The problem of treating the many-body problem lies in the electron-electron interation. In the non-interacting case, $E[n]$ has a kinetic contribution and a contribution from the external potential $V_{ext}$:

$$E[n] = T[n] + \int d^3 r n({\bf r}) V_{\hbox{{ext}}}({\bf r})$$ (150)

The variation of 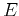$E$ with respect to the density leads to the following equation:

$$\frac{\delta T[n]}{\delta n({\bf r}) } + V_{ext}({\bf r}) = \mu ,$$ (151)

where 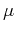$\mu$ is the chemical potential and acts as a Lagrange multiplier associated to the density contraint. The problem with this expression is that we still don not know how to write tthe kinetic energy as a function of the density. Fortunately, we know how to solve the non-interacting case, and the exact ground-state has the form of a Slater determinant. The correspoding Schrödinger equation reads:

$$\left[-\frac{1}{2}\nabla ^2 + V_{ext}({\bf r}) \right] \psi_k({\bf r}) = \epsilon_k \psi_k({\bf r}).$$ (152)

The ground-state density of given by

$$n({\bf r}) = \sum_{k=1}^N \vert\psi_k({\bf r})\vert^2,$$ (153)

and this solution is self-consistent.

From the exact solution of the non-interacting case, we know that $T[n]$ is independent of the external potential $V_{ext}$.