


Next: Hohenberg-Kohn theorems
Up: Density Functional Theory
Previous: Functionals and functional derivatives
For the classical part of the potential, Thomas and Fermi employed the Coulomb potential energy functional
![\begin{displaymath}
U[n(r)] = \frac{1}{2}\int\int \frac{n({\bf r}) n({\bf r}')}{\vert \mathbf{r}-\mathbf{r}' \vert} d^3r d^3r'
\end{displaymath}](img346.png) |
(141) |
Again, ![$U[n]$](img347.png) depends only on the charge density
depends only on the charge density  and does not depend on its gradient, Laplacian, or other higher-order derivatives. Therefore,
and does not depend on its gradient, Laplacian, or other higher-order derivatives. Therefore,
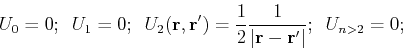 |
(142) |
and we find
![\begin{displaymath}
\frac{\delta U[n]}{\delta n} = \int \frac{n(\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}' \vert} d^3r'
\end{displaymath}](img349.png) |
(143) |
The second functional derivative of the Coulomb potential energy functional is
![\begin{displaymath}
\frac{\delta^2 U[n]}{\delta n^2} = \frac{1}{\vert \mathbf{r}-\mathbf{r}' \vert}
\end{displaymath}](img350.png) |
(144) |
We should make the following observation. Thsi potential contains a self-interaction between a particle and itself, which is unphysical. It does not take into account the Pauli principle, and therefore, this functional should be corrected to cancel the effects of the self-interaction and take exchange into account properly. Notice that this is equivalent to the Hartree potential in the Hartree-Fock approximation.



Next: Hohenberg-Kohn theorems
Up: Density Functional Theory
Previous: Functionals and functional derivatives
Adrian E. Feiguin
2009-11-04
![\begin{displaymath}
U[n(r)] = \frac{1}{2}\int\int \frac{n({\bf r}) n({\bf r}')}{\vert \mathbf{r}-\mathbf{r}' \vert} d^3r d^3r'
\end{displaymath}](img346.png)
![\begin{displaymath}
U[n(r)] = \frac{1}{2}\int\int \frac{n({\bf r}) n({\bf r}')}{\vert \mathbf{r}-\mathbf{r}' \vert} d^3r d^3r'
\end{displaymath}](img346.png)
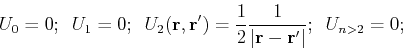
![\begin{displaymath}
\frac{\delta U[n]}{\delta n} = \int \frac{n(\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}' \vert} d^3r'
\end{displaymath}](img349.png)
![\begin{displaymath}
\frac{\delta^2 U[n]}{\delta n^2} = \frac{1}{\vert \mathbf{r}-\mathbf{r}' \vert}
\end{displaymath}](img350.png)