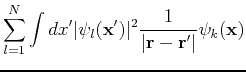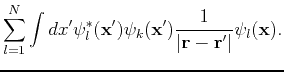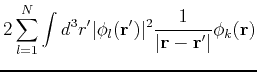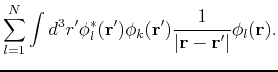Next: Koopman's theorem
Up: Hartree-Fock theory
Previous: Hartree-Fock theory
The full Hartree-Fock equations are given by
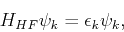 |
(97) |
with
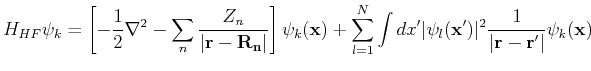 |
|
|
(98) |
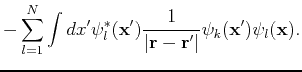 |
|
|
(99) |
Notice that the wavefunctions deppend on the generalize coordinate  , which includes the orbital and spin parts.
The right hand side of the equations consists of four terms. The first and second give rise are the kinetic energy contribution and the electron-ion potential. The third term, or Hartree term, is the simply electrostatic potential arising from the charge distribution of
, which includes the orbital and spin parts.
The right hand side of the equations consists of four terms. The first and second give rise are the kinetic energy contribution and the electron-ion potential. The third term, or Hartree term, is the simply electrostatic potential arising from the charge distribution of 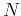 electrons. As written, the term includes an unphysical self-interaction of electrons when
electrons. As written, the term includes an unphysical self-interaction of electrons when  . This term is cancelled in the fourth, or exchange term. The exchange term results from our inclusion of the Pauli principle and the assumed determinantal form of the wavefunction.
Notice that thsi term is non-local, its value at
. This term is cancelled in the fourth, or exchange term. The exchange term results from our inclusion of the Pauli principle and the assumed determinantal form of the wavefunction.
Notice that thsi term is non-local, its value at 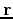 is determined by the value assumed by
is determined by the value assumed by 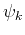 at all possible positions
at all possible positions 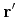 .
.
We can rewrite 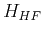 as the sum of different terms:
as the sum of different terms:
 |
(100) |
with
We can eliminate the sum over the spin indices by summing over them, to find the operators acting on the orbital part, only. The 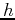 operators remains the same since it does not contain any spin dependence. The new operators
operators remains the same since it does not contain any spin dependence. The new operators 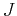 and
and 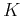 acting on the orbital parts then read:
acting on the orbital parts then read:
Multiplying by
 and integrating over
and integrating over 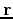 we obtain the expression for the energy:
we obtain the expression for the energy:
 |
(106) |
where the factors 2 arise from the sum over the spin indices.



Next: Koopman's theorem
Up: Hartree-Fock theory
Previous: Hartree-Fock theory
Adrian E. Feiguin
2009-11-04
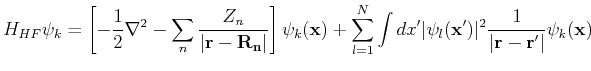
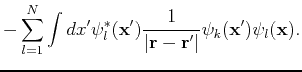
![]() as the sum of different terms:
as the sum of different terms:
![$\displaystyle \sum_i \left[-\frac{1}{2}\nabla_i^2-\sum_n \frac{Z_n}{\vert{\bf r_i}-{\bf R_n}\vert}\right]$](img276.png)