


Next: General case: the many
Up: Many electron systems and
Previous: Many electron systems and
In the helium problem, we could make use of the fact that in the ground-state, the antisymmetry is taken care of by the spin part of the wave-function, whcih in turn drops out of the Schrödinger equation.
If we are after excited states, or if more than two electrons are involved, the antisymmetry requirement affects the orbital part of the wave-function and must be taken into account.
Let us take another look at the two-particle case.
The simplest way to approximate the wave function of a many-particle system is to take the product of properly chosen wave functions of the individual particles. For the two-particle case, we have
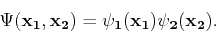 |
(86) |
This expression is used in the Hartree method as an ansatz for the many-particle wave function and is known as a Hartree product. However, it is not satisfactory for fermions, such as electrons, because the wave function is not antisymmetric. An antisymmetric wave function can be mathematically described as follows:
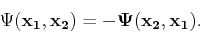 |
(87) |
Therefore the Hartree product does not satisfy the Pauli principle. This problem can be overcome by taking a linear combination of both Hartree products
 |
(88) |
where the coefficient is the normalization factor. This wave function is antisymmetric and no longer distinguishes between fermions. Moreover, it also goes to zero if any two wave functions or two fermions are the same. This is equivalent to satisfying the Pauli exclusion principle.
If we now take into account the spin degree of freedom
 , we obtain:
, we obtain:
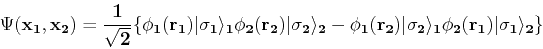 |
(89) |



Next: General case: the many
Up: Many electron systems and
Previous: Many electron systems and
Adrian E. Feiguin
2009-11-04

![]() , we obtain:
, we obtain: