We would like to develop an algorithm to generate all the possible configurations of world lines, that is ergodic, and does not violate the conservation rules. The conservation of ![]() implies the fololowing restrictions: if two spins are moved on a horizontal side of an interacting plaquette, they must necessarily be anti-parallel; if two spins on a lateral side participate, they can only move if they point in the same direction.
implies the fololowing restrictions: if two spins are moved on a horizontal side of an interacting plaquette, they must necessarily be anti-parallel; if two spins on a lateral side participate, they can only move if they point in the same direction.
We mus generate all the possible closed loops under these considerations applying all the possible moved compatible with the torus topology. The toroidal geometry is a consequence of the preiodic boundary conditions in the space direction (to preserva translational invariance) and along the time direction (required by the trace operation). The minimum local move tthat we can make corresponds to moving two parallel spins from one side of a non-interacting plaquette, to the opposite side, as illustrated in Fig.[]. Perdoming successive changes of this kind it is possible to generate all the possible configurations with a given ``winding number'', conserving the total value of ![]() . We define ``winding number'' of a given configuration of worldlines in the following way: Since we are evaluating the trace with periodic boundary conditions, the system has the topology of a torus. Suppose that we start from an arbitrary site at
. We define ``winding number'' of a given configuration of worldlines in the following way: Since we are evaluating the trace with periodic boundary conditions, the system has the topology of a torus. Suppose that we start from an arbitrary site at ![]() with spin
with spin ![]() , and we follow the worldline continuously for an entire revolution along the time direction (
, and we follow the worldline continuously for an entire revolution along the time direction (![]() grows from 0 to
grows from 0 to ![]() , and returns to 0). If we arrive to the same site after a revolution, we say that tthe configuration has a winding number equal to zero; if we require
, and returns to 0). If we arrive to the same site after a revolution, we say that tthe configuration has a winding number equal to zero; if we require ![]() revolutions to return to the same site, we then say that the configuration has a winding number equal to
revolutions to return to the same site, we then say that the configuration has a winding number equal to ![]() , with the sign depending on the spatial direction we move with each revolution. In the majority of the cases, only configurations with winding number zero are important. Configurations with larger winding number can only be obtained with periodic boundary conditions, althoug it is clear that they do not occur with open boundary conditions.
, with the sign depending on the spatial direction we move with each revolution. In the majority of the cases, only configurations with winding number zero are important. Configurations with larger winding number can only be obtained with periodic boundary conditions, althoug it is clear that they do not occur with open boundary conditions.
The Monte Carlo algorithm we need to devise will consists of different possible moves. The local move, similar to the ``flipping'' move for the Ising model, would correspond to sweeping over all the sites of the lattice, and verifying that it is possible to move a worldline accross a white plaquette. If a white plaquette has its lower-left corner on site ![]() ) of the lattice, a move will only be possible if the quantity
) of the lattice, a move will only be possible if the quantity
![]() . A possitive sign allows to move the line from left to right, while for a negative sign, from right to left. Is a move is possible, we need to calculate the transition probablity as the ratio between the matrix elements of the involved plaquettes, before, and after the move, for instance:
. A possitive sign allows to move the line from left to right, while for a negative sign, from right to left. Is a move is possible, we need to calculate the transition probablity as the ratio between the matrix elements of the involved plaquettes, before, and after the move, for instance:
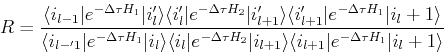 |
(298) |
| (299) |
Since we only take into account two possible configurations of world lines, we emply the "thermal bath'' algorithm to accept or reject new configurations. Therefore, we accept or not a new configuration with probability
| (300) |
Besides the local moves, there are two other types of global moves necessary to preserve ergodicity. The first one is responsible for the fluctuations in the magnetization and is illustrated in Fig.[]. We look for a straight line of spins pointing in the same direction, and we flip all of them simultaneously. This allows one to calculate values of the magnetization and the uniform susceptibility, which is generated by magnetic fluctuations of straight lines connecting configurations with different total magnetization. In studies of ground state properties, we require to simulate very low temperatures, and the magnetic fluctuations are negligible or null, and we can ignore them completely, working in the subspace restricted to zero magnetization.
The other global move extends along the spatial direction, and is shown in Fig.[]. Its is responsible of connecting subspaces with different topology, that differ in the winding number. The absence of this type of moves can introduce finite size effects in small systems, but in sufficiently large lattices, they can be ignored.