


Next: Oscillatory Motion
Up: Motion in a central
Previous: Exercise 2.3
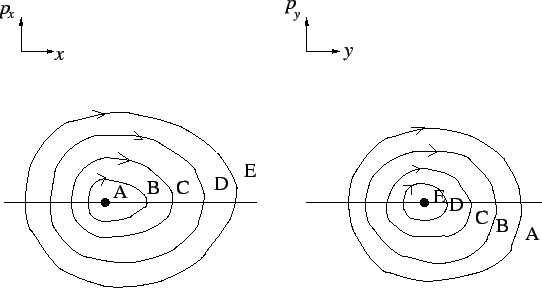
Figure 6:
Trajectories of a particle in a two-dimensional separable
potential as they appear in the 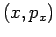 and
and 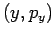 planes.
Several trajectories corresponding to the same energy but different
initial conditions are shown. Trajectories A and E area the limiting
ones having vanishing
planes.
Several trajectories corresponding to the same energy but different
initial conditions are shown. Trajectories A and E area the limiting
ones having vanishing  and
and 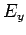 , respectively
, respectively
 |
Let's ``complicate'' things a little bit.
We know that all the problems described above can be expressed
elegantly using the Hamiltonian formalism. Let us consider a particle
of mass 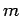 moving in a potential
moving in a potential 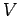 in two dimensions ans assume that
in two dimensions ans assume that
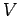 is such that the particle remains confined if the energy is low
enough. The momenta conjugate to the two coordinates
is such that the particle remains confined if the energy is low
enough. The momenta conjugate to the two coordinates 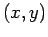 area
area
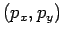 . The Hamiltonian (the energy!) takes the form
. The Hamiltonian (the energy!) takes the form
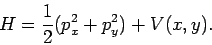 |
(37) |
Given any particular initial values of the coordinates and momenta, the
particle's trajectory is specifies by their time evolution, that is
governed by four first-order differential equations (Hamilton's
equations):
| |
|
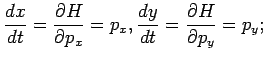 |
(38) |
| |
|
 |
(39) |
For any 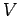 , these equations conserve the energy
, these equations conserve the energy 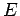 so that the
constraint
so that the
constraint
restricts the trajectory to a three-dimensional manifold embedded in the
four dimensional phase space.
The Hamiltonian is said to be ``integrable'' when there is a second
function of the coordinates and momenta that is also a constant of
motion; the motion is thus constrained to a two-dimensional manifold
in phase space. Two familiar kinds of integrable systems are separable and central potentials.
In the separable case
where  are independent functions of only one variable, so that
the Hamiltonian separates in two parts and
each coordinate can be solved independently,
are independent functions of only one variable, so that
the Hamiltonian separates in two parts and
each coordinate can be solved independently,
The motions of 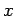 and
and 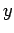 are therefore decoupled form each other and
each of the Hamiltonians is separately a constant of motion.
are therefore decoupled form each other and
each of the Hamiltonians is separately a constant of motion.
In the case of a central potential,
so that the angular momentum 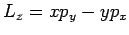 is the second constant of
motion and the Hamiltonian can be written as
is the second constant of
motion and the Hamiltonian can be written as
where 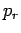 is the momentum conjugate to
is the momentum conjugate to 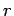 . The additional constraint
on the trajectory makes the system tractable reducing the problem to
les variables. All the familiar analytically soluble problems in
classical mechanics are those that are integrable.
An analysis of phase space suggests a way to detect integrability.
Consider for instance the case of a separable potential, Because the
motions of each of the two coordinates are independent, plots of the
trajectory in
. The additional constraint
on the trajectory makes the system tractable reducing the problem to
les variables. All the familiar analytically soluble problems in
classical mechanics are those that are integrable.
An analysis of phase space suggests a way to detect integrability.
Consider for instance the case of a separable potential, Because the
motions of each of the two coordinates are independent, plots of the
trajectory in 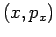 and
and 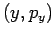 planes should look as in
Fig.6. Here, we assumed that each potential has a
minimum value of 0 at particular values of
planes should look as in
Fig.6. Here, we assumed that each potential has a
minimum value of 0 at particular values of 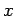 and
and 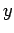 respectively.
The particle moves on a closed contour in each of these two-dimensional
projections of the four-dimensional phase space, each of them looking
as a on-dimensional motion. The areas of these contours is associated
to the total energy (
respectively.
The particle moves on a closed contour in each of these two-dimensional
projections of the four-dimensional phase space, each of them looking
as a on-dimensional motion. The areas of these contours is associated
to the total energy ( and
and 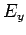 ). Since the total energy must be
conserved, as one varies the initial conditions, one contour shrinks,
and the other grows. In each plane there is a limiting contour that is
approached when all the energy is in one coordinate. The fact that
these contours are closed signals the integrability of the system.
). Since the total energy must be
conserved, as one varies the initial conditions, one contour shrinks,
and the other grows. In each plane there is a limiting contour that is
approached when all the energy is in one coordinate. The fact that
these contours are closed signals the integrability of the system.
How can we obtain this information from the trajectory alone? Supouse
that at every time we observe one of the coordinates, say 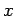 , pass
through zero, we plot the location of the particle in the
, pass
through zero, we plot the location of the particle in the 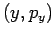 plane. If the periods of the
plane. If the periods of the 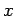 and
and 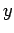 motions are incommensurate
(i.e. their ratio is an irrational number), then, as the
trajectory proceeds, these observations will trace out the full
motions are incommensurate
(i.e. their ratio is an irrational number), then, as the
trajectory proceeds, these observations will trace out the full
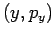 contour; if the periods are commensurate (i.e. a
rational ratio), then a series of discrete points around the contour
will result.
contour; if the periods are commensurate (i.e. a
rational ratio), then a series of discrete points around the contour
will result.



Next: Oscillatory Motion
Up: Motion in a central
Previous: Exercise 2.3
Adrian E. Feiguin
2004-06-01


![]() moving in a potential
moving in a potential ![]() in two dimensions ans assume that
in two dimensions ans assume that
![]() is such that the particle remains confined if the energy is low
enough. The momenta conjugate to the two coordinates
is such that the particle remains confined if the energy is low
enough. The momenta conjugate to the two coordinates ![]() area
area
![]() . The Hamiltonian (the energy!) takes the form
. The Hamiltonian (the energy!) takes the form
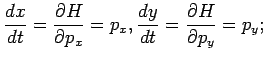

![]() , pass
through zero, we plot the location of the particle in the
, pass
through zero, we plot the location of the particle in the ![]() plane. If the periods of the
plane. If the periods of the ![]() and
and ![]() motions are incommensurate
(i.e. their ratio is an irrational number), then, as the
trajectory proceeds, these observations will trace out the full
motions are incommensurate
(i.e. their ratio is an irrational number), then, as the
trajectory proceeds, these observations will trace out the full
![]() contour; if the periods are commensurate (i.e. a
rational ratio), then a series of discrete points around the contour
will result.
contour; if the periods are commensurate (i.e. a
rational ratio), then a series of discrete points around the contour
will result.