


Next: Trajectories in phase space
Up: Scattering by a central
Previous: Scattering by a central
- Before beginning any numerical computation, it is important to
have some
idea of what the results should look like. Sketch what you think the
deflection function should look like at relatively low energies,
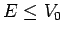 , where the the peripheral collisions at large
, where the the peripheral collisions at large
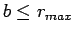 will take place in a predominantly attractive potential and
the more central collisions will ``bounce'' against the repulsive
core.
What happens at much higher energies
will take place in a predominantly attractive potential and
the more central collisions will ``bounce'' against the repulsive
core.
What happens at much higher energies 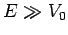 , where the attractive
pocket in
, where the attractive
pocket in 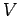 can be neglected? Note that the values of
can be neglected? Note that the values of 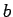 where the
deflection function has a maximum or a minimum, Eq. (35)
shows that the cross section should be infinite,as occurs in the
rainbow formed when light scatters from water drops.
where the
deflection function has a maximum or a minimum, Eq. (35)
shows that the cross section should be infinite,as occurs in the
rainbow formed when light scatters from water drops.
- Write a program that calculates, for a given kinetic energy
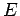 ,
the deflection function solving the equations of motion a a number of
equally spaced
,
the deflection function solving the equations of motion a a number of
equally spaced 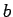 values between 0 and
values between 0 and 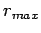 .
.
- Use your program to calculate the deflection function for
scattering from a Lennard-Jones potential at selected values of
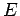 ranging from
ranging from 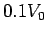 to
to 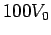 . Reconcile your answers in step 1)
with the results obtained. Calculate the differential cross sections
a function of
. Reconcile your answers in step 1)
with the results obtained. Calculate the differential cross sections
a function of 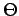 at these energies.
at these energies.
- If your program is working correctly you should observe for
energies
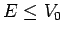 a singularity in the deflection function where
a singularity in the deflection function where
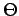 appear to approach
appear to approach 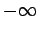 at some critical value of
at some critical value of 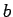 ,
,
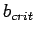 , that depends on
, that depends on 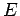 . This singularity, which disappears
when
. This singularity, which disappears
when 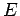 becomes larger that about
becomes larger that about 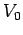 is characteristic of
"orbiting", and the scattering angle becomes logarithmically infinite.
What happens is that the particle spends a very long time spiralling
around the center. Calculate some trajectories around this point and
convince yourself that this is precisely what's happening. Determine
the maximum energy for which the Lennard-Jones potential exhibits
orbiting by solving the correct set of equations involving
is characteristic of
"orbiting", and the scattering angle becomes logarithmically infinite.
What happens is that the particle spends a very long time spiralling
around the center. Calculate some trajectories around this point and
convince yourself that this is precisely what's happening. Determine
the maximum energy for which the Lennard-Jones potential exhibits
orbiting by solving the correct set of equations involving 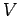 and its
derivatives.
and its
derivatives.



Next: Trajectories in phase space
Up: Scattering by a central
Previous: Scattering by a central
Adrian E. Feiguin
2004-06-01